题目内容
已知正△ABC的边长为3,D、E分别是边BC上的三等分点〔如图(1)所示〕.沿AD、AE把△ABC折成三棱锥A—DEF,使B、C两点重合于点F〔如图(2)〕,且G是DE的中点.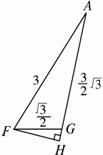
(1)求证:DE⊥平面AGF;
(2)求二面角A-DE-F的大小;
(3)求点F到平面ADE的距离.
(1)证明:在△ADE中,AD=AE,G为DE中点,∴AG⊥DE.?
同理,在△FDE中,FG⊥DE.?
又∵FG∩AG=G,∴DE⊥面AGF.?
(2)解析:由(1)知同∠AGF即为所求二面角的平面角.AF=3,AG=![]() ,DG=
,DG=![]() ,FD=1,FG=
,FD=1,FG=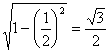 .?
.?
cos∠AGF=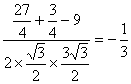 .?
.?
∴∠AGF=π-arccos![]() .?
.?
(3)解析:过F作FH⊥AG于H.?

∵DE⊥面AGF,DE![]() 面ADE,?
面ADE,?
∴面AFG⊥面ADE.?
又∵交线为AG,?
∴FH⊥面ADE,AF=3,FG=![]() ,AG=
,AG=![]() .?
.?
设HG=x,则FH2=AF2-AH2=FG2-GH2,即9-(![]() +x)2=
+x)2=![]() -x2
-x2 ![]() x=
x=![]() .?
.?
FH=![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知正△ABC的边长为
,则到三个顶点的距离都为1的平面有( )
4
| ||
| 3 |
| A、1个 | B、3个 | C、5个 | D、7个 |