题目内容
若函数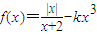
有三个不同的零点，则实数k的取值范围为 ．
【答案】分析：先可判断k一定不是0，进而可得到函数的一定零点；再由等x≠0时，将函数f（x）有零点转化为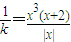
有个两相异的非零实根的问题，即为函数
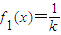与
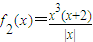图象有两不同的交点，然后画出函数f2（x）的图象求出最小值即可确定k的范围．
解答：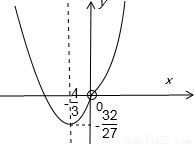
解：当k=0时，不合题意．x=0显然为函数的一个零点．
x≠0时，转化为方程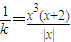
有个两相异的非零实根，
亦即函数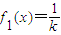
与
图象有两不同的交点．
由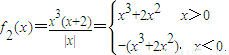
，
在直角坐标系中画出其图象，结合图象不难得出结论．
故答案为：{k|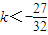
或k＞0}．
点评：本题主要考查函数零点与方程的根的关系，考查以形助数的思想．要充分理解并要灵活运用函数的零点与方程的根、函数与x轴的交点的横坐标一致性．
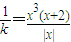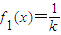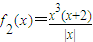有个两相异的非零实根的问题，即为函数与图象有两不同的交点，然后画出函数f2（x）的图象求出最小值即可确定k的范围．解答：
解：当k=0时，不合题意．x=0显然为函数的一个零点．x≠0时，转化为方程
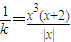有个两相异的非零实根，亦即函数
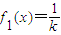与图象有两不同的交点．由
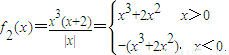，在直角坐标系中画出其图象，结合图象不难得出结论．
故答案为：{k|
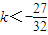或k＞0}．点评：本题主要考查函数零点与方程的根的关系，考查以形助数的思想．要充分理解并要灵活运用函数的零点与方程的根、函数与x轴的交点的横坐标一致性．
练习册系列答案
阅读快车系列答案
相关题目
(其中a,b为实常数)。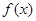
的单调区间：
时，函数
：
上是减函数，设关于x的方程
的两个非零实数根为
，
。试问是否存在实数m,使得
对任意满足条件的a及t
恒成立？若存在，求m的取值范围；若不存在，请说明理由。
是非零常数，关于
的方程
有且仅有三个不同的实数根，若
分别是三个根中的最小根和最大根，则
=
．
，M是非零常数，关于X的方程f（x）=m（m∈R）有且仅有三个不同的实数根，若b、a分别是三个根中的最小根和最大根，则
= ．