Question

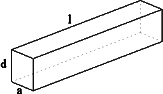
一根水平放置的长方形枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比.

（1）将此枕木翻转90°（即宽度变为厚度），枕木的安全负荷变大吗？为什么？

（2）现取一根横断面为半圆（半圆的半径为R）的木材，用它来截取长方形枕木，其长度即为枕木规定的长度，问如何截取，可使安全负荷最大？

Answer 1

思路分析：此题字母较多，1）需仔细审题利用正比和反比引入比例系数合理地表示出两种安全负荷;2）做第(2)问时，要合理地选取自变量，建立函数模型，可以以截面中长方形的长来作变量，也可以选取角度来作变量，选取方式不同，简繁也是不同的.

解：（1）安全负荷y₁=k·(k＞0)，翻转后为

y₂=k·.∵,∴当0＜d＜a时，y₁＜y₂;当0＜a＜d时，y₁＞y₂.

（2）设横截面的宽为a，高为d,则a²+4d²=R².∵枕木的长度不变，∴u=ad²最大时，安全负荷最大.

u=

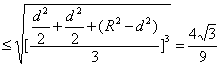R³.

当且仅当=R²-d²,即d=R,a=R时取等号，即安全负荷最大.