题目内容
已知椭圆 的左焦点为F1(-1,0),点F1关于直线16x+12y-9=0对称点在椭圆上.
的左焦点为F1(-1,0),点F1关于直线16x+12y-9=0对称点在椭圆上.(I)求椭圆方程;
(II)点M(x,y)在圆x2+y2=b2上,M在第一象限,过M作圆x2+y2=b2的切线交椭圆于P、Q两点,问|F2P|+|F2Q|+|PQ|是否为定值?如果是,求出定值,如不是,说明理由.

【答案】分析:(I)由已知中椭圆 的左焦点为F1(-1,0),可得c值,点F1关于直线16x+12y-9=0对称点在椭圆上可得a值,进而求出b值后,可得椭圆方程;
的左焦点为F1(-1,0),可得c值,点F1关于直线16x+12y-9=0对称点在椭圆上可得a值,进而求出b值后,可得椭圆方程;
(II)设P(x1,y1),Q(x2,y2),分别求出|F2P|,|F2Q|,结合相切的条件可得|PM|2=|OP|2-|OM|2求出|PQ|,可得结论.
解答:解:(I)∵右焦点为F2(1,0)∴c=1
左焦点为F1(-1,0),点
在椭圆上
∴a=2,
所以椭圆方程为 -------------------------------------(4分)
-------------------------------------(4分)
(II)设P(x1,y1),Q(x2,y2)


∴ --------------------------------------------------------.(7分)
--------------------------------------------------------.(7分)
连接OM,OP,由相切条件知:

∴ ---------------------------------------------------.(10分)
---------------------------------------------------.(10分)
同理可求

所以|F2P|+|F2Q|+|PQ|=2+2=4为定值.-------------------------------------------(12分)
点评:本题考查的知识点是椭圆的标准方程,直线与圆的位置关系,直线与椭圆的位置关系,熟练掌握椭圆的性质是解答本题的关键.
 的左焦点为F1(-1,0),可得c值,点F1关于直线16x+12y-9=0对称点在椭圆上可得a值,进而求出b值后,可得椭圆方程;
的左焦点为F1(-1,0),可得c值,点F1关于直线16x+12y-9=0对称点在椭圆上可得a值,进而求出b值后,可得椭圆方程;(II)设P(x1,y1),Q(x2,y2),分别求出|F2P|,|F2Q|,结合相切的条件可得|PM|2=|OP|2-|OM|2求出|PQ|,可得结论.
解答:解:(I)∵右焦点为F2(1,0)∴c=1
左焦点为F1(-1,0),点

在椭圆上

∴a=2,

所以椭圆方程为
 -------------------------------------(4分)
-------------------------------------(4分)(II)设P(x1,y1),Q(x2,y2)


∴
 --------------------------------------------------------.(7分)
--------------------------------------------------------.(7分)连接OM,OP,由相切条件知:

∴
 ---------------------------------------------------.(10分)
---------------------------------------------------.(10分)同理可求

所以|F2P|+|F2Q|+|PQ|=2+2=4为定值.-------------------------------------------(12分)
点评:本题考查的知识点是椭圆的标准方程,直线与圆的位置关系,直线与椭圆的位置关系,熟练掌握椭圆的性质是解答本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 的左焦点为F,O为坐标原点.
的左焦点为F,O为坐标原点.
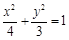 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
 ,求直线AB的斜率;
,求直线AB的斜率; 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C, ,其中圆心P的坐标为
,其中圆心P的坐标为 .
. ,求
,求 上,求椭圆的方程.
上,求椭圆的方程. 的左焦点为F,右顶点为A,点B在椭圆上,且
的左焦点为F,右顶点为A,点B在椭圆上,且 轴,直线AB交
轴,直线AB交 轴于点P。若
轴于点P。若 ,则椭圆的离心率为
,则椭圆的离心率为