题目内容
某车间生产某种产品,固定成本为2万元,每生产一件产品成本增加100元,已知总收益R(总收益指工厂出售产品的全部收入,它是成本与总利润的和,单位:元)是年产量Q(单位:件)的函数,并且满足下面关系式:
R=f(Q)=
,求每年生产多少产品时,总利润最大?此时总利润是多少元?
R=f(Q)=
|
分析:由题设条件知y=R-100Q-20000=
(Q∈Z),由此进行分类讨论能够求出每年生产多少产品时,总利润最大,并能求出此时总利润.
|
解答:解:∵y=R-100Q-20000
=
(Q∈Z),
∴0≤Q≤400时,
y=300Q-
Q2-20000
=-
(Q-300)2+25000,
此时,Q=300时,ymax=25000.
Q>400时,y=60000-100Q<20000.
所以,每年生产300件时利润最大,最大值为25000元.
=
|
∴0≤Q≤400时,
y=300Q-
| 1 |
| 2 |
=-
| 1 |
| 2 |
此时,Q=300时,ymax=25000.
Q>400时,y=60000-100Q<20000.
所以,每年生产300件时利润最大,最大值为25000元.
点评:本题考查函数最值的应用,综合性强,难度大,易出错.解题时要认真审题,注意分类讨论思想的灵活运用.

练习册系列答案
相关题目
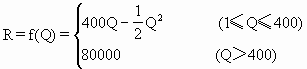
 ,求每年生产多少产品时,总利润最大?此时总利润是多少元?
,求每年生产多少产品时,总利润最大?此时总利润是多少元?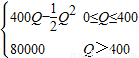 ,求每年生产多少产品时,总利润最大?此时总利润是多少元?
,求每年生产多少产品时,总利润最大?此时总利润是多少元?