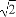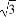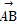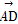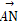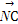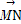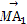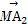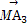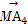Question

已知非零向量e1,e2,a,b满足a=2e1-e2,b=ke1+e2.给出以下结论:

①若e1与e2不共线,a与b共线,则k=-2;

②若e1与e2不共线,a与b共线,则k=2;

③存在实数k,使得a与b不共线,e1与e2共线;

④不存在实数k,使得a与b不共线,e1与e2共线.

其中正确结论的个数是(　　)

(A)1个(B)2个(C)3个(D)4个

 

Answer 1

B

【解析】(1)若a与b共线,即a=λb,即2e1-e2=λke1+λe2,而e1与e2不共线,

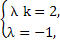∴解得k=-2.故①正确,②不正确.

(2)若e1与e2共线,则e2=λe1,有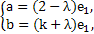

∵e1,e2,a,b为非零向量,∴λ≠2且λ≠-k,

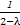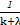∴a=b,即a=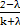b,这时a与b共线,

∴不存在实数k满足题意.故③不正确,④正确.

综上,正确的结论为①④.