题目内容
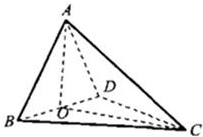 如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=
如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=| 2 |
(1)求证:AO⊥平面BCD;
(2)求异面直线AB与CD所成角的大小;
(3)求二面角O-AC-D的大小.
分析:(1)设O是等腰直角三角形ABD斜边BD的中点,通过正三角形,以及计算证明AO⊥CO,从而证明AO⊥平面BCD;
(2)利用三面角公式直接求异面直线AB与CD所成角的大小的余弦,然后求出角的大小;
(3)利用射影面的面积与被射影面的面积的比,求二面角O-AC-D的大小.
(2)利用三面角公式直接求异面直线AB与CD所成角的大小的余弦,然后求出角的大小;
(3)利用射影面的面积与被射影面的面积的比,求二面角O-AC-D的大小.
解答: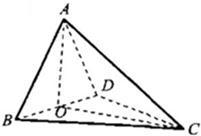 解:(1)设O是等腰直角三角形ABD斜边BD的中点,
解:(1)设O是等腰直角三角形ABD斜边BD的中点,
所以有AO⊥BD,可求得AO=1,CO=
,又有AC=2
所以∠AEC=90°,即AO⊥CO
BD,CO是平面BCD内两条相交直线,故有AO⊥平面BCD.
(2)由(1)可知BD⊥面AOC,
所以面BCD⊥面AOC,AO=1,CO=
,AC=2
A点在BCD面内的投影为O,
cos<AB,CD>=cos∠ABD•cos∠BDC=
×
=
异面直线AB与CD所成角的大小:arccos
.
(3)三角形AOC的面积为:
×AO×OC=
;三角形ADC的面积为:
×
×
=
;
所以二面角O-AC-D的大小余弦为:
=
二面角O-AC-D的大小:arccos
 解:(1)设O是等腰直角三角形ABD斜边BD的中点,
解:(1)设O是等腰直角三角形ABD斜边BD的中点,所以有AO⊥BD,可求得AO=1,CO=
| 3 |
所以∠AEC=90°,即AO⊥CO
BD,CO是平面BCD内两条相交直线,故有AO⊥平面BCD.
(2)由(1)可知BD⊥面AOC,
所以面BCD⊥面AOC,AO=1,CO=
| 3 |
A点在BCD面内的投影为O,
cos<AB,CD>=cos∠ABD•cos∠BDC=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
异面直线AB与CD所成角的大小:arccos
| ||
| 4 |
(3)三角形AOC的面积为:
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| 2 |
22-(
|
| ||
| 2 |
所以二面角O-AC-D的大小余弦为:
| ||||
|
| ||
| 14 |
二面角O-AC-D的大小:arccos
| ||
| 14 |
点评:本小题主要考查空间线面关系、二面角的度量、直线与平面所成的角等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD= 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.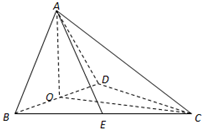 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.