题目内容
以正方体八个顶点中的n个点作为顶点,组成新的空间几何体.按照以下要求分别画出图形:
(1)有一个顶点处三个面都是直角的直角锥体;
(2)各面都是等边三角形的锥体;
(3)各面都是直角三角形的锥体.
(1)有一个顶点处三个面都是直角的直角锥体;
(2)各面都是等边三角形的锥体;
(3)各面都是直角三角形的锥体.
分析:借助正方体图形,比较容易画出符合要求的三棱锥,
解答:解:以正方体八个顶点中的n个点作为顶点,组成新的空间几何体.
(1)有一个顶点处三个面都是直角的直角锥体,如图1三棱锥A-BCD,定点C处△ABC、△ADC、△BCD都是直角三角形的直角棱锥;
图1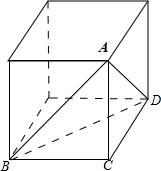
(2)各面都是等边三角形的锥体,如图2三棱锥A-BDE,面ABD、面ABE、面ADE、面BDE都是等边三角形;
图2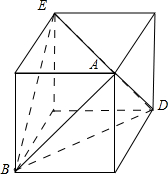
(3)各面都是直角三角形的锥体,如图3三棱锥B-CEF,△BCF、△BEF、△BCE、△CEF都是直角三角形;
图3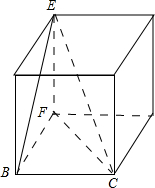
(1)有一个顶点处三个面都是直角的直角锥体,如图1三棱锥A-BCD,定点C处△ABC、△ADC、△BCD都是直角三角形的直角棱锥;
图1

(2)各面都是等边三角形的锥体,如图2三棱锥A-BDE,面ABD、面ABE、面ADE、面BDE都是等边三角形;
图2

(3)各面都是直角三角形的锥体,如图3三棱锥B-CEF,△BCF、△BEF、△BCE、△CEF都是直角三角形;
图3

点评:本题借助于正方体、三棱锥,考查学生的空间思维能力和画图能力,是基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
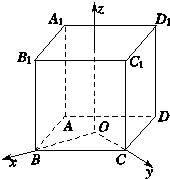
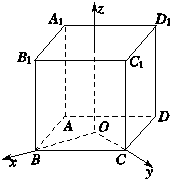 如图,在棱长为2的正方体ABCD-A1B1C1D1中,以底面正方形ABCD的中心为坐标原点O,分别以射线OB,OC,AA1的指向为x轴、y轴、z轴的正方向,建立空间直角坐标系.试写出正方体八个顶点的坐标.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,以底面正方形ABCD的中心为坐标原点O,分别以射线OB,OC,AA1的指向为x轴、y轴、z轴的正方向,建立空间直角坐标系.试写出正方体八个顶点的坐标.