题目内容
在以O为原点的平面直角坐标系中,有点A(4,-3).已知△OAB是直角三角形,∠A=90°,且|AB|=2|OA|,其中点B的纵坐标大于零.
(1)求点B的坐标;
(2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程.
答案:
解析:
解析:
|
解:(1)设点B的坐标为(a,b),由题意,知|OA|=5.又因为|AB|=2|OA|,所以|AB|=10,|OB|=5 所以 解得 因为点B的纵坐标大于零, 所以点B的坐标为(10,5). (2)由点斜式得,直线OB的方程为x-2y=0.将已知圆的方程化为(x-3)2+(y+1)2=10,故圆心的坐标为(3,-1),半径长为 则 解得x=1,y=3.故所求圆的方程为(x-1)2+(y-3)2=10. |

练习册系列答案
相关题目

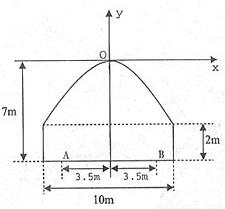
 如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.