题目内容
6名同学安排到3个宿舍,每个宿舍两人,其中甲必须在一号宿舍,乙和丙均不能到三号宿舍,则不同的安排方法种数为
- A.6
- B.9
- C.12
- D.18
B
分析:根据一号宿舍中的安排分类计数,最后将每类的计数结果相加即可
解答:第一类,一号宿舍有丙或乙,共有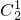 ×
×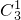 =6种排法;
=6种排法;
第二类,一号宿舍没有丙和乙,共有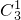 =3种排法;
=3种排法;
故所有可能的排法有6+3=9种
故选 B
点评:本题主要考查了计数的方法,分类计数原理和分步计数原理的应用,排列组合数公式的应用,属基础题
分析:根据一号宿舍中的安排分类计数,最后将每类的计数结果相加即可
解答:第一类,一号宿舍有丙或乙,共有
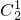 ×
×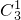 =6种排法;
=6种排法;第二类,一号宿舍没有丙和乙,共有
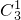 =3种排法;
=3种排法;故所有可能的排法有6+3=9种
故选 B
点评:本题主要考查了计数的方法,分类计数原理和分步计数原理的应用,排列组合数公式的应用,属基础题

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目