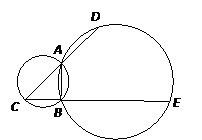题目内容
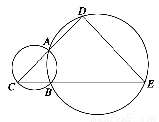
如图,A、B是两圆的交点,AC是小圆的直径,D和E分别是CA和CB的延长线与大圆的交点,已知AC=4,BE=10,且BC=AD,求DE的长.
【答案】
6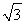
【解析】
试题分析:设CB=AD=x,根据割线定理可以得出CA·CD=CB·CE,代入数值可以算出x=2,然后利用圆的内接四边形对角互补,有CD2+DE2=CE2,从而算出DE=6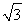 .
.
试题解析:设CB=AD=x,则由割线定理得:CA·CD=CB·CE,即4(4+x)=x(x+10)
化简得x2+6x-16=0,解得x=2或x=-8(舍去) ,即CD=6,CE=12.
因为CA为直径,所以∠CBA=90°,即∠ABE=90°,则由圆的内接四边形对角互补,得∠D=90°,
则CD2+DE2=CE2,∴62+DE2=122,∴DE=6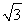
考点:1.割线定理;2.圆内接四边形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
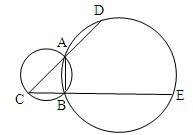
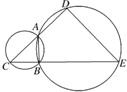
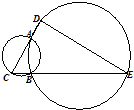 (几何证明选讲选做题) 如图,A、B是两圆的交点,AC是小圆的直径,D和E分别是CA和CB的延长线与大圆的交点,已知AC=4,BE=10,且BC=AD,则DE=
(几何证明选讲选做题) 如图,A、B是两圆的交点,AC是小圆的直径,D和E分别是CA和CB的延长线与大圆的交点,已知AC=4,BE=10,且BC=AD,则DE=