题目内容
已知复数z1=（m2-2m+3）-mi，z2=2m+（m2+m-1）i其中i是虚数单位，m∈R
（1）若z1，z2互为共轭复数，求实数m的值
（2）若z1-z2是负实数，求实数m的取值集合
（3）求|z1+z2|的最小值．
【答案】分析：（1）若 z1，z2互为共轭复数，则有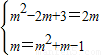
，由此解得，m的值．
（2）化简z1-z2=（m2-4m+3）-（m2+2m-1）i，依题意，有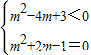
，由此求得所以实数m的取值集合．
（3）化简z1+z2为（m2+3）-（m2-1）i，可得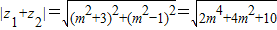
；再利用二次函数的性质求得它的最小值．
解答：解：（1）若 z1，z2互为共轭复数，则有
，…（2分）
解得，m=1．…（4分）
（2）根据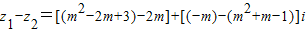
=（m2-4m+3）-（m2+2m-1）i，…（5分）
依题意，有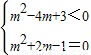
．…（7分）
解得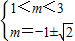
无解，所以实数m的取值集合为∅．…（9分）
（3）
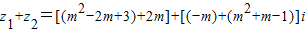=（m2+3）-（m2-1）i．…（10分）
所以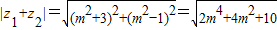
=
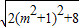．（12分）
因为m2≥0，所以当m2=0时，|z1+z2|取得最小值
．…（14分）
点评：本题主要考查复数的基本概念，复数求模，属于基础题．
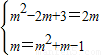，由此解得，m的值．（2）化简z1-z2=（m2-4m+3）-（m2+2m-1）i，依题意，有
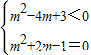，由此求得所以实数m的取值集合．（3）化简z1+z2为（m2+3）-（m2-1）i，可得
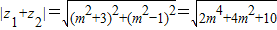；再利用二次函数的性质求得它的最小值．解答：解：（1）若 z1，z2互为共轭复数，则有
，…（2分）解得，m=1．…（4分）
（2）根据
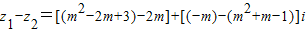=（m2-4m+3）-（m2+2m-1）i，…（5分）依题意，有
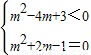．…（7分）解得
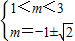无解，所以实数m的取值集合为∅．…（9分）（3）
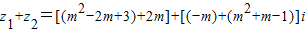=（m2+3）-（m2-1）i．…（10分）所以
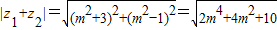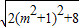=．（12分）因为m2≥0，所以当m2=0时，|z1+z2|取得最小值
．…（14分）点评：本题主要考查复数的基本概念，复数求模，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目