题目内容
(2013•临沂一模)已知数列{an}的前n项和Sn满足Sn+an+(
)n-1=2(n∈N*),设cn=2nan.
(I)求证:数列{cn}是等差数列,并求数列{an}的通项公式;
(II)按以下规律构造数列{bn},具体方法如下:b1=c1,b2=c2+c3,b3=c4+c5+c6+c7,…第n项bn由相应的{cn}中2n-1项的和组成,求数列{bn}的通项bn.
| 1 | 2 |
(I)求证:数列{cn}是等差数列,并求数列{an}的通项公式;
(II)按以下规律构造数列{bn},具体方法如下:b1=c1,b2=c2+c3,b3=c4+c5+c6+c7,…第n项bn由相应的{cn}中2n-1项的和组成,求数列{bn}的通项bn.
分析:(I)由Sn+an+(
)n-1=2知,当n=1时可求得a1,当n≥2时,可求得2nan-2n-1an-1=1,由cn=2nan,可得数列{cn}是等差数列,从而可求得其通项公式;
(II)依题意,bn=c2n-1+c2n-1+1+c2n-1+2+…+c2n-1=2n-1+(2n-1+1)+(2n-1+2)+…+(2n-1),利用等差数列的求和公式即可求得答案.
| 1 |
| 2 |
(II)依题意,bn=c2n-1+c2n-1+1+c2n-1+2+…+c2n-1=2n-1+(2n-1+1)+(2n-1+2)+…+(2n-1),利用等差数列的求和公式即可求得答案.
解答:解:(I)在Sn+an+(
)n-1=2①中,令n=1,
得:S1+a1+1=2,
∴a1=
.
当n≥2时,Sn-1+an-1+(
)n-2=2,②
①-②得:2an-an-1-(
)n-1=0,(n≥2),…2
∴2an-an-1=(
)n-1,
∴2nan-2n-1an-1=1…3分
又cn=2nan,
∴cn-cn-1=1(n≥2),又c1=2a1=1,
∴数列{cn}是等差数列,…4分
∴cn=1+(n-1)×1=n,又cn=2nan,
∴an=
…6分
(II)由题意得
bn=c2n-1+c2n-1+1+c2n-1+2+…+c2n-1…7分
=2n-1+(2n-1+1)+(2n-1+2)+…+(2n-1)…8分
而2n-1,2n-1+1,2n-1+2,…,2n-1是首项为2n-1,公差为1的等差数列,
设数列共有2n-1项,…9分,
所以,bn=
=
=3×22n-3-2n-2…12分
| 1 |
| 2 |
得:S1+a1+1=2,
∴a1=
| 1 |
| 2 |
当n≥2时,Sn-1+an-1+(
| 1 |
| 2 |
①-②得:2an-an-1-(
| 1 |
| 2 |
∴2an-an-1=(
| 1 |
| 2 |
∴2nan-2n-1an-1=1…3分
又cn=2nan,
∴cn-cn-1=1(n≥2),又c1=2a1=1,
∴数列{cn}是等差数列,…4分
∴cn=1+(n-1)×1=n,又cn=2nan,
∴an=
| n |
| 2n |
(II)由题意得
bn=c2n-1+c2n-1+1+c2n-1+2+…+c2n-1…7分
=2n-1+(2n-1+1)+(2n-1+2)+…+(2n-1)…8分
而2n-1,2n-1+1,2n-1+2,…,2n-1是首项为2n-1,公差为1的等差数列,
设数列共有2n-1项,…9分,
所以,bn=
| [2n-1+(2n-1)]×2n-1 |
| 2 |
=
| 22n-2+22n-1-2n-1 |
| 2 |
=3×22n-3-2n-2…12分
点评:本题考查数列的求和,着重考查等差数列的通项公式与求和公式,(II)中bn=2n-1+(2n-1+1)+(2n-1+2)+…+(2n-1)的确定是难点,考查观察与推理分析的能力,属于难题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
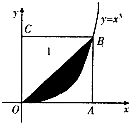 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )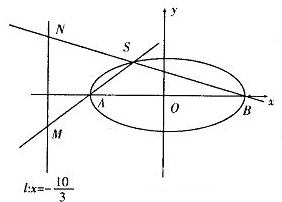 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: