题目内容
(本小题满分12分)已知斜率为1的直线 与双曲线
与双曲线 相交于B、D两点,且BD的中点为M(1,3)。
相交于B、D两点,且BD的中点为M(1,3)。
(1)求双曲线C的离心率;
(2)若双曲线C的右焦点坐标为(3,0),则以双曲线的焦点为焦点,过直线 上一点M作椭圆,要使所作椭圆的长轴最短,点M应在何处?并求出此时的椭圆方程。
上一点M作椭圆,要使所作椭圆的长轴最短,点M应在何处?并求出此时的椭圆方程。
【答案】
(本小题满分12分)
解:(Ⅰ)由题设知: 的方程为
的方程为 ,代入
,代入 的方程,并化简得:
的方程,并化简得:
 (*)…………………………2分
(*)…………………………2分
设 ,则
,则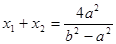 ,
, ……4分
……4分
由 为
为 的中点知
的中点知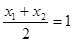 ,故
,故
即 . 故
. 故 , ∴
, ∴ 验证可知方程(*)的△>0………6分
验证可知方程(*)的△>0………6分
(Ⅱ)双曲线的左、右焦点为 、
、 ,点
,点 关于直线
关于直线 ①
①
的对称点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 ② ………8分
② ………8分
解方程组①②得:交点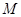
 ……………………………9分
……………………………9分
此时 最小,所求椭圆的长轴
最小,所求椭圆的长轴 ,
,
∴ …………………………………………………………11分
…………………………………………………………11分
又 , ∴
, ∴ ,故所求椭圆的方程为
,故所求椭圆的方程为 ………………12分
………………12分
【解析】略

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目