题目内容
已知函数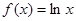
(Ⅰ)若 ,求
,求 的极大值;
的极大值;
(Ⅱ)若 在定义域内单调递减,求满足此条件的实数k的取值范围.
在定义域内单调递减,求满足此条件的实数k的取值范围.
【答案】
(Ⅰ)F(x)取得极大值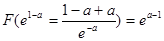 .(Ⅱ)
.(Ⅱ)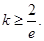
【解析】
试题分析:(Ⅰ)利用“求导数,求驻点,讨论驻点左右区间的单调性,求极值”.
(Ⅱ)由G (x)在定义域内单调递减知: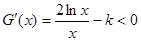 在(0+∞)内恒成立.
在(0+∞)内恒成立.
通过构造函数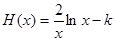 ,利用导数研究函数的单调性,确定H(x)取最大值
,利用导数研究函数的单调性,确定H(x)取最大值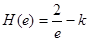
由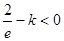 恒成立,确定得到实数k的取值范围.
恒成立,确定得到实数k的取值范围.
试题解析:(Ⅰ) 定义域为
定义域为
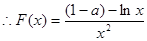 2分
2分
令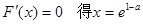 由
由
由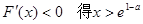 4分
4分
即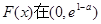 上单调递增,在
上单调递增,在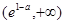 上单调递减
上单调递减
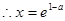 时,F(x)取得极大值
时,F(x)取得极大值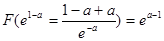 6分
6分
(Ⅱ)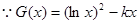 的定义域为(0+∞)
的定义域为(0+∞) 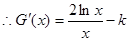
由G (x)在定义域内单调递减知: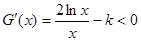 在(0+∞)内恒成立 8分
在(0+∞)内恒成立 8分
令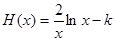 ,则
,则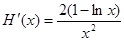 由
由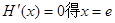
∵当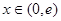 时
时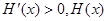 为增函数
为增函数
当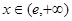 时
时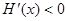
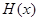 为减函数
10分
为减函数
10分
∴当x = e时,H(x)取最大值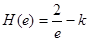
故只需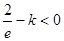 恒成立,
恒成立,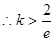
又当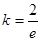 时,只有一点x = e使得
时,只有一点x = e使得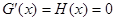 不影响其单调性
不影响其单调性
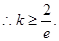 12分
12分
考点:利用导数研究函数的单调性、极值.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 ,
, 
 .
. , 函数
, 函数 在其定义域是增函数,求
在其定义域是增函数,求 的取值范围;
的取值范围; 的最小值;
的最小值; 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点 ,过线段
,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 ,问是否存在点
,问是否存在点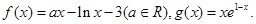
 图象在(0,0)处的切线也恰为
图象在(0,0)处的切线也恰为 图象的一条切线,求实数a的值;
图象的一条切线,求实数a的值; ,都有唯一的
,都有唯一的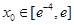 ,使得
,使得 成立,若存在,求出a的取值范围;若不存在,请说明理由。
成立,若存在,求出a的取值范围;若不存在,请说明理由。
 ,求
,求 的单调递减区间;
的单调递减区间; ,求
,求 的最小值;
的最小值; ,且存在
,且存在 使得
使得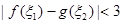 ,求实数
,求实数 的取值范围。
的取值范围。 .
. ,求函数
,求函数 在区间
在区间 的值域;
的值域; 上为增函数,求
上为增函数,求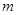 的取值范围.
的取值范围.