题目内容
给出下列命题:
①若“sinα-tanα>0”则“α是第二或第四象限角”;
②平面直角坐标系中有三个点A(4,5),B(-2,2),C(2,0),则tan∠ABC=
;
③若a>1,b>1且lg(a+b)=lga+lgb,则lg(a-1)+lg(b-1)的值为1;
④设[m]表示不大于m的最大整数,若x,y∈R,那么[x+y]≥[x]+[y];
其中所有正确命题的序号是
①若“sinα-tanα>0”则“α是第二或第四象限角”;
②平面直角坐标系中有三个点A(4,5),B(-2,2),C(2,0),则tan∠ABC=
| 4 | 3 |
③若a>1,b>1且lg(a+b)=lga+lgb,则lg(a-1)+lg(b-1)的值为1;
④设[m]表示不大于m的最大整数,若x,y∈R,那么[x+y]≥[x]+[y];
其中所有正确命题的序号是
①④
①④
.分析:①由三角函数的定义可判断
②由KBA=
=
,KBC=
=-2,可得BA⊥BC;
③由已知可得a+b=ab,而(a-1)(b-1)=ab-(a+b)+1=1,则lg(a-1)+lg(b-1)=0
④分x,y为整数和小数分别讨论可判断求解
②由KBA=
| 2-5 |
| -2-4 |
| 1 |
| 2 |
| 2+2 |
| 0-2 |
③由已知可得a+b=ab,而(a-1)(b-1)=ab-(a+b)+1=1,则lg(a-1)+lg(b-1)=0
④分x,y为整数和小数分别讨论可判断求解
解答:解:①由三角函数的定义可得,当“sinα-tanα>0”则“α是第二或第四象限角”;正确
②平面直角坐标系中有三个点A(4,5),B(-2,2),C(2,0),KBA=
=
,KBC=
=-2,
则可得BA⊥BC;②错误
③由a>1,b>1且lg(a+b)=lga+lgb,可得a+b=ab,则lg(a-1)+lg(b-1)=lg(a-1)(b-1)
而(a-1)(b-1)=ab-(a+b)+1=1,则lg(a-1)+lg(b-1)=0,;③错误
④若x,y至少一个为整数时,[x+y]=[x]+[y];当x,y不是整数时,若x=a.b,y=c.d(a,b分别为x,y的整数,c,d分别为x,y的小数位),若b+d>1时,[x+y]>[x]+[y],若c+d≤1,则[x+y]=[x}+[y],从而有[x+y]>[x]+[y],④正确
故答案为:①④
②平面直角坐标系中有三个点A(4,5),B(-2,2),C(2,0),KBA=
| 2-5 |
| -2-4 |
| 1 |
| 2 |
| 2+2 |
| 0-2 |
则可得BA⊥BC;②错误
③由a>1,b>1且lg(a+b)=lga+lgb,可得a+b=ab,则lg(a-1)+lg(b-1)=lg(a-1)(b-1)
而(a-1)(b-1)=ab-(a+b)+1=1,则lg(a-1)+lg(b-1)=0,;③错误
④若x,y至少一个为整数时,[x+y]=[x]+[y];当x,y不是整数时,若x=a.b,y=c.d(a,b分别为x,y的整数,c,d分别为x,y的小数位),若b+d>1时,[x+y]>[x]+[y],若c+d≤1,则[x+y]=[x}+[y],从而有[x+y]>[x]+[y],④正确
故答案为:①④
点评:本题主要考查了三角函数的定义、直线的斜率公式及由斜率判断直线的位置关系,对数的基本运算性质的应用.

练习册系列答案
相关题目
 、
、 ,两个不同平面
,两个不同平面 、
、 ,给出下列命题:
,给出下列命题:
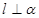 ,则
,则 则
则 在平面
在平面 。
。 ,对任意
,对任意 ,运算“
,运算“ ”具有如下性质:
”具有如下性质: ; (2)
; (2) ; (3)
; (3) .
. :
: ,则
,则 ;
; ,且
,且 ,则a = 0;
,则a = 0; ,且
,且 ,
, ,则a = c.
,则a = c. 和
和 为不重合的两个平面,给出下列命题:1若
为不重合的两个平面,给出下列命题:1若 与
与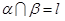 ,若
,若 ;4直线
;4直线 的充要条件是
的充要条件是 、
、 ,且m⊥
,且m⊥ ,
,