题目内容
函数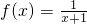
的图象与直线x=0，x=1以及x轴围成的曲边梯形的面积是
- A.0
- B.1
- C.e
- D.ln2
D
分析：先根据题意画出区域，然后依据图形得到积分上限为1，积分下限为0，从而利用定积分表示出曲边梯形的面积，最后用定积分的定义求出所求即可．
解答：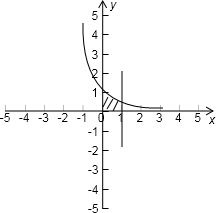
解：先根据题意画出图形，得到积分上下限
函数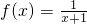的图象与直线x=0，x=1以及x轴围成的曲边梯形的面积是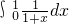
而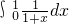=ln（x+1）|01=ln2
∴曲边梯形的面积是ln2
故选D．
点评：考查学生会求出原函数的能力，以及会利用定积分求图形面积的能力，同时考查了数形结合的思想，属于基础题．
分析：先根据题意画出区域，然后依据图形得到积分上限为1，积分下限为0，从而利用定积分表示出曲边梯形的面积，最后用定积分的定义求出所求即可．
解答：
解：先根据题意画出图形，得到积分上下限函数
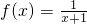的图象与直线x=0，x=1以及x轴围成的曲边梯形的面积是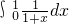而
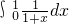=ln（x+1）|01=ln2∴曲边梯形的面积是ln2
故选D．
点评：考查学生会求出原函数的能力，以及会利用定积分求图形面积的能力，同时考查了数形结合的思想，属于基础题．
练习册系列答案
相关题目
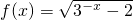的图象与直线x=a，（a∈R）的公共点个数为
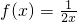的图象与直线x=1，x=e （e是自然对数的底）及x轴围成的平面图形的面积等于
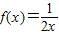的图象与直线x=1，x=e （e是自然对数的底）及x轴围成的平面图形的面积等于（ ）
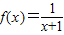的图象与直线x=0，x=1以及x轴围成的曲边梯形的面积是（ ）
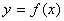定义在[-2，3]上，则函数
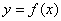的图象与直线x=2的交点个数有