题目内容
 选修4-1:几何证明选讲
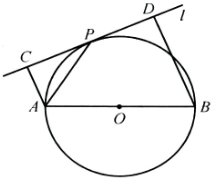
选修4-1:几何证明选讲如图,设直线l切圆O于点P,AB为圆O的任意一条不与l垂直的直径,AC⊥l,BD⊥l,垂足分别为C,D.求证:PC=PD,且AP平分∠CAB.
分析:连结OP,可得OP⊥l,结合题意AC⊥l且BD⊥l,得OP∥AC∥BD,再由平行线的性质结合OA=OB证出PC=PD.△OPA中根据OA=OP得∠OAP=∠APO,由AC∥OP得∠PAC=∠APO,可得∠PAC=∠OAP,即AP平分∠CAB.
解答: 证明:连结OP,
证明:连结OP,
∵直线l与圆O相切于P点,
∴OP⊥l
∵AC⊥l,BD⊥l,
∴OP∥AC∥BD,
∵OA=OB,∴PC=PD,
∵OA=OP,∴∠OAP=∠APO
∵AC∥OP,得∠PAC=∠APO,
∴∠PAC=∠OAP,即AP平分∠CAB.
 证明:连结OP,
证明:连结OP,∵直线l与圆O相切于P点,
∴OP⊥l
∵AC⊥l,BD⊥l,
∴OP∥AC∥BD,
∵OA=OB,∴PC=PD,
∵OA=OP,∴∠OAP=∠APO
∵AC∥OP,得∠PAC=∠APO,
∴∠PAC=∠OAP,即AP平分∠CAB.
点评:本题给出过直径的两端作圆的切线的垂线,求证切点到两个垂足的距离相等,并且证明角相等.着重考查了圆的切线的性质定理、平行线的性质和等腰三角形的性质等知识,属于中档题.

练习册系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲