题目内容
 已知动点A、B分别在图中抛物线y2=4x及椭圆
已知动点A、B分别在图中抛物线y2=4x及椭圆| x2 |
| 4 |
| y2 |
| 3 |
分析:利用用抛物线的焦半径公式和椭圆的焦半径公式来解答,先通过联立抛物线与椭圆方程,求出A,B点的横坐标范围,再利用焦半径公式转换为以B点的横坐标为参数的式子,再根据前面求出的B点横坐标方位计算即可.
解答:解:由抛物线y2=4x及椭圆
+
=1可知,在第一象限的交点横坐标为
,
设A(x1,y1),B(x2,y2),则0<x1<
,
<x2<2,
由可得,三角形ABN的周长l=|AN|+|AB|+|BN|=x1+
+x2-x1+a-ex2=
+a+
x2=3+
x2,
∵
<x2<2,
∴
<3+
x2<4
故选D.
| x2 |
| 4 |
| y2 |
| 3 |
| 2 |
| 3 |
设A(x1,y1),B(x2,y2),则0<x1<
| 2 |
| 3 |
| 2 |
| 3 |
由可得,三角形ABN的周长l=|AN|+|AB|+|BN|=x1+
| p |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵
| 2 |
| 3 |
∴
| 10 |
| 3 |
| 1 |
| 2 |
故选D.
点评:本题考查了抛物线与椭圆焦半径公式的应用,做题时要善于把未知转化为已知.

练习册系列答案
相关题目
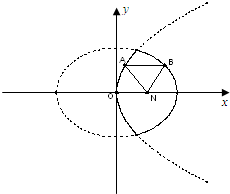 [理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆
[理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆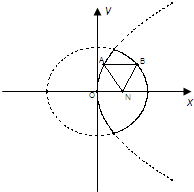 已知动点A、B分别在图中抛物线y2=4x及椭圆
已知动点A、B分别在图中抛物线y2=4x及椭圆 及椭圆
及椭圆 的实线上运动,若
的实线上运动,若 ∥
∥ 轴,点N的坐标
轴,点N的坐标 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.