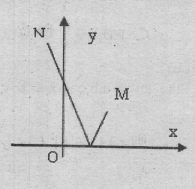题目内容
光线从点M(-2,3)射到x轴上一点后被x轴反射,反射光线所在的直线l1与直线l2:3x-2y+13=0平行,求l1和l2的距离.
由题意可得M(-2,3)关于x轴对称的点M′(-2,-3)(2分)
∵反射光线l1与已知直线l2平行
∴k1=k2=
(4分)
∴直线l1的方程为y+3=
(x+2)即3x-2y=0(6分)
由两平行线间的距离公式,可得d=
=
(9分)
∴所求的直线l1与,l2的距离为
(10分)
∵反射光线l1与已知直线l2平行
∴k1=k2=
| 3 |
| 2 |
∴直线l1的方程为y+3=
| 3 |
| 2 |
由两平行线间的距离公式,可得d=
| |13-0| | ||
|
| 13 |
∴所求的直线l1与,l2的距离为
| 13 |

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
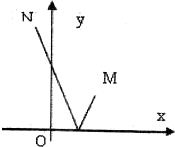
 轴反射后经过N(-1,6),求入射光线所在直线方程。
轴反射后经过N(-1,6),求入射光线所在直线方程。