题目内容
设0<θ<π,
=cosθ+isinθ,则θ的值为
.
1+
| ||
|
| π |
| 6 |
| π |
| 6 |
分析:把给出的等式的左边利用复数的除法运算化简,然后利用复数相等的条件得到cosθ=
,sinθ=
,最后根据角的范围求角.
| ||
| 2 |
| 1 |
| 2 |
解答:解:由
=
=
=
+
i=cosθ+isinθ,
得cosθ=
,sinθ=
,又0<θ<π,∴θ=
.
故答案为:
.
1+
| ||
|
(1+
| ||||
(
|
2
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
得cosθ=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题考查了复数代数形式的乘除运算,考查了复数相等的条件,训练了由三角函数的值求角的方法,是基础题.

练习册系列答案
相关题目
设0≤x<2π,且
=sinx-cosx,则( )
| 1-sin2x |
| A、0≤x≤π | ||||
B、
| ||||
C、
| ||||
D、
|
设集合M={x|x2-x-2<0},P={x∈Z||x-1|≤3},Q={x|x∈P,x∉M},则Q=( )
| A、{-2,1,2,3,4} | B、{-2,-1,2,3,4} | C、{-1,2,3,4} | D、{-1,2,3} |
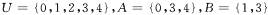 ,则
,则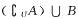 =
=