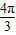题目内容
在锐二面角α-l-β中,A∈α,AB⊥β于B,BC⊥α于C,若AB=6,BC=3.则锐二面角α-l-β的平面角的大小为( )
| A、30° | B、45° | C、60° | D、60°或120° |
分析:由AB⊥β于B可得AB⊥l,同理BC⊥l,所以l⊥平面ABC.设平面ABC交直线l与点O,所以锐二面角α-l-β的平面角为∠ACB.再利用解三角形的有关知识解决问题即可.
解答:解:由题意可得图象如图所示:
因为二面角α-l-β中,AB⊥β于B,所以AB⊥l,
同理BC⊥l,所以l⊥平面ABC.
设平面ABC交直线l与点O,

所以点A、C、O共线,所以锐二面角α-l-β的平面角为∠ACB.
在△ABO中,AB⊥BO,AB=6,BC=3,
所以tan∠ACB=
,
所以锐二面角α-l-β的平面角的大小为60°.
故选C.
因为二面角α-l-β中,AB⊥β于B,所以AB⊥l,
同理BC⊥l,所以l⊥平面ABC.
设平面ABC交直线l与点O,

所以点A、C、O共线,所以锐二面角α-l-β的平面角为∠ACB.
在△ABO中,AB⊥BO,AB=6,BC=3,
所以tan∠ACB=
| 3 |
所以锐二面角α-l-β的平面角的大小为60°.
故选C.
点评:本题主要考查二面角的平面角的有关知识,找出二面角的平面角是解题的难点和关键,了利用解三角形的有关知识求出答案即可.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
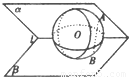
 (2012•乐山二模)如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若AB=
(2012•乐山二模)如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若AB=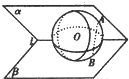 如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若
如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若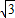 ,球心O到二面角的棱l的距离为2,则球O的表面积为( )
,球心O到二面角的棱l的距离为2,则球O的表面积为( )