题目内容
过圆x2+y2-4x=0外一点P(m,n)作圆的两条切线,当这两条切线互相垂直时,m,n 应满足的关系式为( )A.(m-2)2+n2=4
B.(m+2)2+n2=4
C.(m-2)2+n2=8
D.(m+2)2+n2=8
【答案】分析:把圆的方程化为标准方程,找出圆心坐标和半径r,根据题意画出图形,如图所示,证明四边形PQMN为边长为半径r的正方形,则点P到圆心间的距离为正方形对角线的长,由正方形的边长求出对角线的长,然后由P和M的坐标,利用两点间的距离公式表示出线段PM的长,让其值等于对角线的长,即可得到m与n满足的关系式.
解答:解:把圆的方程化为标准方程:(x-2)2+y2=4,
故圆心坐标为(2,0),半径r=2,
根据题意画出图形,如图所示:
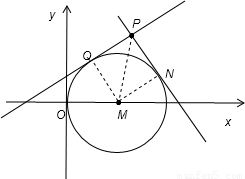
连接MQ,MN,得到∠MQP=∠MNP=90°,又∠QPN=90°,
∴PQMN为矩形,又MQ=MN=2,
∴PQMN为边长为2的正方形,
则|PM|=2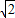 ,即(m-2)2+n2=8.
,即(m-2)2+n2=8.
故选C
点评:此题考查了切线的性质,正方形的性质及两点间的距离公式.通过证明得到四边形PQMN为正方形是解本题的关键,同时注意数形结合数学思想的运用.
解答:解:把圆的方程化为标准方程:(x-2)2+y2=4,
故圆心坐标为(2,0),半径r=2,
根据题意画出图形,如图所示:

连接MQ,MN,得到∠MQP=∠MNP=90°,又∠QPN=90°,
∴PQMN为矩形,又MQ=MN=2,
∴PQMN为边长为2的正方形,
则|PM|=2
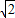 ,即(m-2)2+n2=8.
,即(m-2)2+n2=8.故选C
点评:此题考查了切线的性质,正方形的性质及两点间的距离公式.通过证明得到四边形PQMN为正方形是解本题的关键,同时注意数形结合数学思想的运用.

练习册系列答案
相关题目
过圆x2+y2-4x=0外一点P(m,n)作圆的两条切线,当这两条切线互相垂直时,m,n 应满足的关系式为( )
| A、(m-2)2+n2=4 | B、(m+2)2+n2=4 | C、(m-2)2+n2=8 | D、(m+2)2+n2=8 |