题目内容
已知![]() ,(
,(![]() ),直线
),直线![]() 与函数
与函数![]() 、
、![]() 的图像都相切,且与函数
的图像都相切,且与函数![]() 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(Ⅰ)求直线![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)若![]() (其中
(其中![]() 是
是![]() 的导函数),求函数
的导函数),求函数![]() 的最大值;
的最大值;
(Ⅲ)当![]() 时,求证:
时,求证:![]() .
.
解:(Ⅰ)依题意知:直线![]() 是函数
是函数![]() 在点
在点![]() 处的切线,故其斜率
处的切线,故其斜率
![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
又因为直线![]() 与
与![]() 的图像相切,所以由
的图像相切,所以由
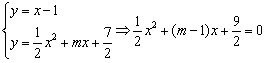 ,
,
得![]() (
(![]() 不合题意,舍去);
不合题意,舍去);
(Ⅱ)因为![]() (
(![]() ),所以
),所以
![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
因此,当![]() 时,
时,![]() 取得最大值
取得最大值![]() ;
;
(Ⅲ)当![]() 时,
时,![]() .由(Ⅱ)知:当
.由(Ⅱ)知:当![]() 时,
时,![]() ,
,
即![]() .因此,有
.因此,有
![]() .
.

练习册系列答案
相关题目
已知函教f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与直线y=b(0<b<A)的三个相邻交点的横坐标分别是2,4,8,则f(x)的单调递增区间是( )
| A、[6kπ,6kπ+3],k∈Z | B、[6k-3,6k],k∈Z | C、[6k,6k+3],k∈Z | D、[6kπ-3,6kπ],k∈Z |
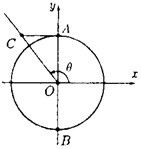 如图,已知单位圆O与y轴相交于A、B两点.角θ的顶点为原点,始边在x轴的正半轴上,终边在射线OC上.过点A作直线AC垂直于y轴且与角θ的终边交于点C,则有向线段AC的函数值是( )
如图,已知单位圆O与y轴相交于A、B两点.角θ的顶点为原点,始边在x轴的正半轴上,终边在射线OC上.过点A作直线AC垂直于y轴且与角θ的终边交于点C,则有向线段AC的函数值是( )| A、sinθ | B、cosθ | C、tanθ | D、cotθ |
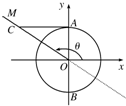 如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?
如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?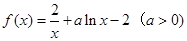 .
.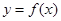 在点
在点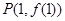 处的切线与直线
处的切线与直线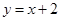 垂直,求函数
垂直,求函数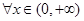 都有
都有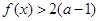 成立,试求
成立,试求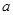 的取值范围;
的取值范围;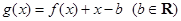 .当
.当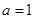 时,函数
时,函数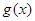 在区间
在区间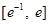 上有两个零点,求实数
上有两个零点,求实数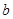 的取值范围.
的取值范围. 的图象与直线y = b (0<b<A)的三个相邻交点的横坐标分别是2,4,8,则
的图象与直线y = b (0<b<A)的三个相邻交点的横坐标分别是2,4,8,则 的单调递增区间是( )
的单调递增区间是( ) B.
B. 
 D.
无法确定
D.
无法确定