题目内容
计算:(1)已知a>0,a2x=3,求
的值;
(2)求
的值.
| a3x+a-3x |
| ax+a-x |
(2)求
| lg8+lg125-lg2-lg5 | ||
lg
|
分析:(1)首先利用立方和公式把分子分解,约分整理成最简形式,把负指数表示的式子化成正指数,把所给的条件代入即可.
(2)把对数中的真数写成指数形式,利用对数的性质,把真数的指数提前,再利用对数的性质进行运算,得到结果.
(2)把对数中的真数写成指数形式,利用对数的性质,把真数的指数提前,再利用对数的性质进行运算,得到结果.
解答:解:(1)原式=
=a2x+
-1=3+
-1=
.
(2)原式=
=
=-4lg10=-4.
| (ax+a-x)(a2x-1+a-2x) |
| ax+a-x |
=a2x+
| 1 |
| a2x |
| 1 |
| 3 |
| 7 |
| 3 |
(2)原式=
| lg23+lg53-lg2-lg5 | ||
|
=
| 2(lg2+lg5) | ||
-
|
点评:本题考查对数的性质和有理指数幂的运算,解题的过程中注意对数性质的应用,这里比较容易出错的还是立方和公式,高中和初中阶段都没有讲解.

练习册系列答案
相关题目
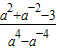 的值.
的值.