题目内容
设x,y,z∈R+且x+y+z=6,则lgx+lgy+lgz的取值范围是 ( )
| A.(-∞,lg6] | B.(-∞,3lg2] |
| C.[lg6,+∞) | D.[3lg2,+∞) |
B
解析选B.因为x,y,z∈R+,
所以6=x+y+z≥3 ,即xyz≤8,
,即xyz≤8,
所以lgx+lgy+lgz=lgxyz≤lg8=3lg2.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
设m>n,n∈N+,x>1,a=(lgx)m+(lgx)-m,b=(lgx)n+(lgx)-n,则a与b的大小关系为
( )
| A.a≥b |
| B.a≤b |
| C.与x的值有关,大小不定 |
| D.以上都不正确 |
若a,b∈(0,+∞),且a≠b,M= +
+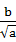 ,N=
,N= +
+ ,则M与N的大小关系是 ( )
,则M与N的大小关系是 ( )
| A.M>N | B.M<N |
| C.M≥N | D.M≤N |
已知在△ABC中,AB=1,BC=2,则∠C的最大值是 ( )
A. | B. | C. | D. |
若不等式x2+|2x-6|≥a对于一切实数x均成立,则实数a的最大值是 ( )
| A.7 | B.9 | C.5 | D.11 |
对于实数x,y,若|x-1|≤1,|y-2|≤1,则|x-2y+1|的最大值为 ( )
| A.5 | B.4 | C.8 | D.7 |
 ,对于一切的
,对于一切的 恒成立,则
恒成立,则 的取值范围是_________。
的取值范围是_________。 ,且
,且 ,则
,则 的最小值为
的最小值为 
 ,n2=
,n2=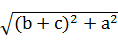 ,n3=
,n3= ,则n1n2,n2n3,
,则n1n2,n2n3, ,
, 中的最小的一个是 .
中的最小的一个是 .