题目内容
设全集U={(x,y)|x,y∈R},集合A={(x,y)|xsinα+ycosα-2=0,α∈R},则在直角平面上集合CuA内所有元素的对应点构成的图形的面积等于
4π
4π
.分析:利用点到直线的距离公式求出原点到集合A中直线xsinα+ycosα-2=0的距离d,发现d为定值,故集合A表示原点到这条直线距离为2的直线系中的直线上的点,全集为平面直角坐标系中的所有点,根据补集的意义可知:集合A的补集表示以原点为圆心,2为半径的圆内部的点,利用圆的面积公式即可求出在直角平面上集合CuA内所有元素的对应点构成的图形的面积.
解答:解:∵原点(0,0)到直线xsinα+ycosα-2=0的距离d=
=2,
∴集合A表示原点到直线距离为2的直线系中的直线,如下图所示:
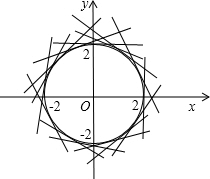
又全集U={(x,y)|x,y∈R},
∴在直角平面上集合CuA内所有元素的对应点构成的图形为半径是2的圆,
则此图形的面积为4π.
故答案为:4π
| 2 | ||
|
∴集合A表示原点到直线距离为2的直线系中的直线,如下图所示:

又全集U={(x,y)|x,y∈R},
∴在直角平面上集合CuA内所有元素的对应点构成的图形为半径是2的圆,
则此图形的面积为4π.
故答案为:4π
点评:此题考查了补集及其运算,涉及的知识有:点到直线的距离公式,同角三角函数间的基本关系,其中根据题意得出在直角平面上集合CuA内所有元素的对应点构成的图形为一个圆是解本题的关键.

练习册系列答案
相关题目
 },B={x|y=ln(1-2x)}.
},B={x|y=ln(1-2x)}.