题目内容
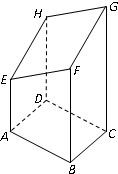 如图是表示以AB=4,BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体,其中四边形EFGH为截面.已知AE=5,BF=8,CG=12.
如图是表示以AB=4,BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体,其中四边形EFGH为截面.已知AE=5,BF=8,CG=12.
(1)作出截面EFGH与底面ABCD的交线l;
(2)截面四边形EFGH是否为菱形?并证明你的结论;
(3)求DH的长.
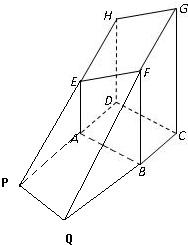
解:(1)根据公里3,作HE与DA的交点P,作GF与CB的交点Q,则点Q是截面EFGH与底面ABCD,
故连PQ得直线l,它便是所求作,如下图:
(2)截面EFGH为菱形.
∵平面ABFE∥平面DCGH,且平面EFGH分别截平面ABFE与平面DCGH得直线EF与GH,∴EF∥GH.
同理,FG∥EH,∴四边形EFGH为平行四边形.
又∵EF2=AB2+(BF-AE)2=25,FG2=BC2+(CG-BF)2=25,∴EF=FG=5,
∴四边形EFGH为菱形.
(3)∵几何体是长方体被一平面斜截所得的,
∴AE+CG=BF+DH,把AE=5,BF=8,CG=12代入得,DH=9.
分析:(1)根据公里3分别作出两个平面的公共点,连接这两个点所成的直线,即是所求的直线;
(2)根据平面ABFE∥平面DCGH和面面平行的限制定理得EF∥GH,再由FG∥EH得四边形EFGH为平行四边形,由题意求出EF=FG,即证出结论;
(3)根据几何体的结构特征得AE+CG=BF+DH,代入数据求出DH的长.
点评:本题考查了简单几何体的结构特征,考查了面面平行性质定理的应用,利用勾股定理求线段的长度,利用公里3作两个平面的交线,考查了观察能力和空间想象能力.
故连PQ得直线l,它便是所求作,如下图:

(2)截面EFGH为菱形.
∵平面ABFE∥平面DCGH,且平面EFGH分别截平面ABFE与平面DCGH得直线EF与GH,∴EF∥GH.
同理,FG∥EH,∴四边形EFGH为平行四边形.
又∵EF2=AB2+(BF-AE)2=25,FG2=BC2+(CG-BF)2=25,∴EF=FG=5,
∴四边形EFGH为菱形.
(3)∵几何体是长方体被一平面斜截所得的,
∴AE+CG=BF+DH,把AE=5,BF=8,CG=12代入得,DH=9.
分析:(1)根据公里3分别作出两个平面的公共点,连接这两个点所成的直线,即是所求的直线;
(2)根据平面ABFE∥平面DCGH和面面平行的限制定理得EF∥GH,再由FG∥EH得四边形EFGH为平行四边形,由题意求出EF=FG,即证出结论;
(3)根据几何体的结构特征得AE+CG=BF+DH,代入数据求出DH的长.
点评:本题考查了简单几何体的结构特征,考查了面面平行性质定理的应用,利用勾股定理求线段的长度,利用公里3作两个平面的交线,考查了观察能力和空间想象能力.

练习册系列答案
相关题目
 15、如图是表示以AB=4,BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体,其中四边形EFGH为截面.已知AE=5,BF=8,CG=12.
15、如图是表示以AB=4,BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体,其中四边形EFGH为截面.已知AE=5,BF=8,CG=12. 通常用a、b、c分别表示△ABC的三个内角A,B,C所对边的边长,R表示△ABC的外接圆半径.
通常用a、b、c分别表示△ABC的三个内角A,B,C所对边的边长,R表示△ABC的外接圆半径. (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)