题目内容
设函数f(x)=sin(2π+ϕ)(-π<ϕ<0),y=f(x)图象的一条对称轴是直线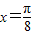 .
.(Ⅰ)求ϕ;
(Ⅱ)求函数y=f(x)的单调增区间;
(Ⅲ)证明直线5x-2y+c=0与函数y=f(x)的图象不相切.
【答案】分析:(Ⅰ)y=f(x)图象的一条对称轴是直线 .就是
.就是 时函数取得最值,结合ϕ的范围,求出ϕ的值;
时函数取得最值,结合ϕ的范围,求出ϕ的值;
(Ⅱ)利用正弦函数的单调增区间,直接求函数y=f(x)的单调增区间;
(Ⅲ)利用导数求出导函数的值域,从而证明直线5x-2y+c=0与函数y=f(x)的图象不相切.
解答:解:(Ⅰ)∵x= 是函数y=f(x)的图象的对称轴,
是函数y=f(x)的图象的对称轴,
∴ ,∴
,∴ ,k∈Z.
,k∈Z.
∵-π<ϕ<0,ϕ=- .
.
(Ⅱ)由(Ⅰ)知ϕ=- ,因此
,因此 .
.
由题意得2kπ- ,k∈Z.
,k∈Z.
所以函数 的单调增区间为
的单调增区间为 .
.
(Ⅲ)证明:∵|y'|= =
= ,
,
所以曲线y=f(x)的切线斜率取值范围为[-2,2],
而直线5x-2y+c=0的斜率为 >2,
>2,
所以直线5x-2y+c=0与函数 的图象不相切.
的图象不相切.
点评:本小题主要考查三角函数性质及图象的基本知识,考查推理和运算能力.是综合题,常考题型.
 .就是
.就是 时函数取得最值,结合ϕ的范围,求出ϕ的值;
时函数取得最值,结合ϕ的范围,求出ϕ的值;(Ⅱ)利用正弦函数的单调增区间,直接求函数y=f(x)的单调增区间;
(Ⅲ)利用导数求出导函数的值域,从而证明直线5x-2y+c=0与函数y=f(x)的图象不相切.
解答:解:(Ⅰ)∵x=
 是函数y=f(x)的图象的对称轴,
是函数y=f(x)的图象的对称轴,∴
 ,∴
,∴ ,k∈Z.
,k∈Z.∵-π<ϕ<0,ϕ=-
 .
.(Ⅱ)由(Ⅰ)知ϕ=-
 ,因此
,因此 .
.由题意得2kπ-
 ,k∈Z.
,k∈Z.所以函数
 的单调增区间为
的单调增区间为 .
.(Ⅲ)证明:∵|y'|=
 =
= ,
,所以曲线y=f(x)的切线斜率取值范围为[-2,2],
而直线5x-2y+c=0的斜率为
 >2,
>2,所以直线5x-2y+c=0与函数
 的图象不相切.
的图象不相切.点评:本小题主要考查三角函数性质及图象的基本知识,考查推理和运算能力.是综合题,常考题型.

练习册系列答案
相关题目