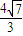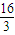题目内容
已知双曲线过点(4,
),渐近线方程为y=±
x,圆C经过双曲线的一个顶点和一个焦点且圆心在双曲线上,则圆心到该双曲线的中心的距离是
.
4
| ||
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
| 16 |
| 3 |
分析:求出双曲线方程,可得双曲线的顶点、焦点,从而可得圆心坐标,即可求圆心到该双曲线的中心的距离.
解答:解:由题意,设双曲线方程为
-
=λ
∵双曲线过点(4,
),∴λ=1
∴双曲线的方程为
-
=1,
∴双曲线的顶点为(±3,0),焦点为(±5,0).
又圆心在双曲线上,所以圆C应过左顶点、左焦点或右顶点、右焦点,即圆心的横坐标为±4,
设圆心的纵坐标为m,则
-
=1,
所以m2=
,
所以所求的距离为
=
.
故答案为:
.
| x2 |
| 9 |
| y2 |
| 16 |
∵双曲线过点(4,
4
| ||
| 3 |
∴双曲线的方程为
| x2 |
| 9 |
| y2 |
| 16 |
∴双曲线的顶点为(±3,0),焦点为(±5,0).
又圆心在双曲线上,所以圆C应过左顶点、左焦点或右顶点、右焦点,即圆心的横坐标为±4,
设圆心的纵坐标为m,则
| 16 |
| 9 |
| m2 |
| 16 |
所以m2=
| 112 |
| 9 |
所以所求的距离为
(±4)2+
|
| 16 |
| 3 |
故答案为:
| 16 |
| 3 |
点评:本题考查双曲线的性质和应用,解题时要注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
已知双曲线过点(4,
),渐近线方程为y=±
x,圆C经过双曲线的一个顶点和一个焦点且圆心在双曲线上,则圆心到该双曲线的中心的距离是( )
4
| ||
| 3 |
| 4 |
| 3 |
A、
| ||||
B、
| ||||
| C、4 | ||||
D、
|
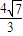 ),渐近线方程为y=±
),渐近线方程为y=± x,圆C经过双曲线的一个顶点和一个焦点且圆心在双曲线上,则圆心到该双曲线的中心的距离是 .
x,圆C经过双曲线的一个顶点和一个焦点且圆心在双曲线上,则圆心到该双曲线的中心的距离是 .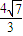 ),渐近线方程为y=±
),渐近线方程为y=± x,圆C经过双曲线的一个顶点和一个焦点且圆心在双曲线上,则圆心到该双曲线的中心的距离是( )
x,圆C经过双曲线的一个顶点和一个焦点且圆心在双曲线上,则圆心到该双曲线的中心的距离是( )