题目内容
设函数y=x3与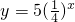
的图象交点为P（x0，y0），则x0所在的区间是
- A.（0，1）
- B.（1，2）
- C.（2，3）
- D.（3，4）
B
分析：令f（x）=x3-5•
，则由题意可得，x0 就是函数f（x）的零点，由函数零点的判定定理求得x0所在的区间．
解答：令f（x）=x3-5•，则由题意可得，x0 就是函数f（x）的零点．
由于f（1）=1-
=-
＜0，f（2）=8-
＞0，故x0所在的区间是（1，2），
故选B．
点评：本题主要考查函数的零点和方程的根的关系和零点存在性定理，考查考生的灵活转化能力和对零点存在性定理的理解，属于基础题．
分析：令f（x）=x3-5•
，则由题意可得，x0 就是函数f（x）的零点，由函数零点的判定定理求得x0所在的区间．解答：令f（x）=x3-5•
，则由题意可得，x0 就是函数f（x）的零点．由于f（1）=1-
=-＜0，f（2）=8-＞0，故x0所在的区间是（1，2），故选B．
点评：本题主要考查函数的零点和方程的根的关系和零点存在性定理，考查考生的灵活转化能力和对零点存在性定理的理解，属于基础题．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
设函数y=x3与y=（
）x-2的图象的交点为（x0，y0），则x0所在的区间是（ ）
| 1 |
| 2 |
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
设函数y=x3与y=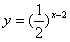
的图象的交点为(x0，y0)，则x0所在的区间是