题目内容
已知集合,A={x|ax+b•2x-1<0,0≤a≤2,1≤b≤3},集合B={x|-1≤x≤0},若a,b∈N,则A∩B≠∅的概率为
.
| 7 |
| 9 |
| 7 |
| 9 |
分析:根据题意,分析a、b可得(a,b)的情况,令函数f(x)=ax+b•2x-1,x∈[-1,0],求导分析单调性可得其最小值,要使A∩B≠∅,只须-a+
-1<0,分析可得(a,b)能取的情况数,进而由几何概型的意义可得答案;
| b |
| 2 |
解答: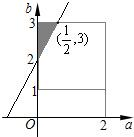 解:(1)因为a,b∈N,且0≤a≤2,1≤b≤3,
解:(1)因为a,b∈N,且0≤a≤2,1≤b≤3,
(a,b)可取(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),
(2,1),(2,2),(2,3)共9组.
令函数f(x)=ax+b•2x-1,x∈[-1,0],则f′(x)=a+bln2•2x.
因为a∈[0,2],b∈[1,3],所以f'(x)>0,即f(x)在[-1,0]上是单调增函数.
f(x)在[-1,0]上的最小值为-a+
-1.
要使A∩B≠∅,只须-a+
-1<0,即2a-b+2>0.
所以(a,b)只能取(0,1),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)7组.
所以A∩B≠∅的概率为
.
故答案为:
.
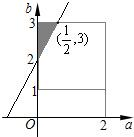 解:(1)因为a,b∈N,且0≤a≤2,1≤b≤3,
解:(1)因为a,b∈N,且0≤a≤2,1≤b≤3,(a,b)可取(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),
(2,1),(2,2),(2,3)共9组.
令函数f(x)=ax+b•2x-1,x∈[-1,0],则f′(x)=a+bln2•2x.
因为a∈[0,2],b∈[1,3],所以f'(x)>0,即f(x)在[-1,0]上是单调增函数.
f(x)在[-1,0]上的最小值为-a+
| b |
| 2 |
要使A∩B≠∅,只须-a+
| b |
| 2 |
所以(a,b)只能取(0,1),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)7组.
所以A∩B≠∅的概率为
| 7 |
| 9 |
故答案为:
| 7 |
| 9 |
点评:本题重点考查几何概型的意义与几何概型的计算,解题时注意a、b的范围,考查计算能力.

练习册系列答案
相关题目
 已知集合,
已知集合,