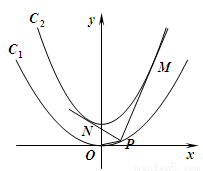
题目内容
如图,已知抛物线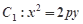 的焦点在抛物线
的焦点在抛物线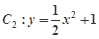 上.
上.
(1)求抛物线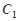 的方程及其准线方程;
的方程及其准线方程;
(2)过抛物线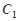 上的动点
上的动点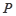 作抛物线
作抛物线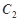 的两条切线
的两条切线 、
、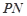 , 切点为
, 切点为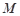 、
、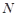 .若
.若 、
、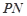 的斜率乘积为
的斜率乘积为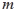 ,且
,且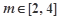 ,求
,求 的取值范围.
的取值范围.
【答案】
(1) 的方程为
的方程为 ,其准线方程为
,其准线方程为 (2)
(2)
【解析】
试题分析:(1) 的焦点为
的焦点为 ,
,
所以 ,
, .
.
故 的方程为
的方程为 ,其准线方程为
,其准线方程为  .
.
(2)任取点 ,设过点P的
,设过点P的 的切线方程为
的切线方程为 .
.
由 ,得
,得 .
.
由 ,化简得
,化简得 ,
,
记 斜率分别为
斜率分别为 ,则
,则 ,
,
因为 ,所以
,所以
所以 ,
,
所以
考点:抛物线方程及支线与抛物线的位置关系
点评:当出现函数曲线在某一点处的切线时,常首先设出切点坐标,利用导数的几何意义(函数在某一点处的导数值等于该点处的切线斜率)求出切线斜率写出切线方程

练习册系列答案
相关题目
 的焦点在抛物线
的焦点在抛物线 上.
上.
 的方程及其准线方程;
的方程及其准线方程; 作抛物线
作抛物线 的两条切线
的两条切线 、
、 , 切点为
, 切点为 、
、 .若
.若 ,且
,且 ,求
,求 的取值范围.
的取值范围.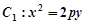 的焦点在抛物线
的焦点在抛物线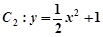 上,点
上,点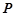 是抛物线
是抛物线 上的动点.
上的动点.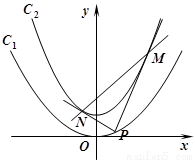
 的两条切线,
的两条切线, 、
、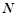 分别为两个切点,设点
分别为两个切点,设点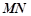 的距离为
的距离为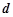 ,求
,求 的焦点F恰好是双曲线
的焦点F恰好是双曲线 的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
 B.
B. C.
C. D.
D. 
 如图,已知抛物线
如图,已知抛物线 的焦点在抛物线
的焦点在抛物线 上,点P是抛物线C1上的动点.
上,点P是抛物线C1上的动点.