题目内容
某工艺品厂要生产如图所示的一种工艺品,该工艺品由一个圆柱和一个半球组成,要求半球的半径和圆柱的底面半径之比为3:2,工艺品的体积为34πcm3.设圆柱的底面直径为4x(cm),工艺品的表面积为S(cm2).
(1)试写出S关于x的函数关系式;
(2)怎样设计才能使工艺品的表面积最小?
(1)试写出S关于x的函数关系式;
(2)怎样设计才能使工艺品的表面积最小?

(1)由题知圆柱的底面半径为2x,半球的半径为3x.
设圆柱的高为h(cm).因为工艺品的体积为34πcm3,所以
×
(3x)3+π(2x)2h=34π,
所以h=
-
x,所以工艺品的表面积为
S=
×4π(3x)2+2π(2x)h+π(3x)2+2×π(2x)2
=35πx2+4πx(
-
x)
=17π(x2+
).
由x>0且h=
-
x>0,得0<x<
.
所以S关于x的函数关系式是S=17π(x2+
),0<x<
.
(2)由(1)知,S′=17π(2x-
)=
,0<x<
.令S'=0,得x=1.
当0<x<1时,S'<0,所以S关于x∈(0,1]是单调减函数;
当1<x<
时,S'>0,所以S关于x∈[1,
)是单调增函数.
所以,当x=1时,S取得最小值Smin=17π(12+
)=51π,此时h=4.
答:按照圆柱的高为4cm,圆柱的底面半径为2cm,半球的半径为3cm设计,工艺品的表面积最小,为51πcm2.
设圆柱的高为h(cm).因为工艺品的体积为34πcm3,所以
| 1 |
| 2 |
| 4 |
| 3 |
所以h=
| 17 |
| 2x2 |
| 9 |
| 2 |
S=
| 1 |
| 2 |
=35πx2+4πx(
| 17 |
| 2x2 |
| 9 |
| 2 |
=17π(x2+
| 2 |
| x |
由x>0且h=
| 17 |
| 2x2 |
| 9 |
| 2 |
| |||
| 3 |
所以S关于x的函数关系式是S=17π(x2+
| 2 |
| x |
| |||
| 3 |
(2)由(1)知,S′=17π(2x-
| 2 |
| x |
| 34π(x3-1) |
| x2 |
| |||
| 3 |
当0<x<1时,S'<0,所以S关于x∈(0,1]是单调减函数;
当1<x<
| |||
| 3 |
| |||
| 3 |
所以,当x=1时,S取得最小值Smin=17π(12+
| 2 |
| 1 |
答:按照圆柱的高为4cm,圆柱的底面半径为2cm,半球的半径为3cm设计,工艺品的表面积最小,为51πcm2.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
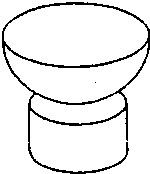 某工艺品厂要生产如图所示的一种工艺品,该工艺品由一个圆柱和一个半球组成,要求半球的半径和圆柱的底面半径之比为3:2,工艺品的体积为34πcm3.设圆柱的底面直径为4x(cm),工艺品的表面积为S(cm2).
某工艺品厂要生产如图所示的一种工艺品,该工艺品由一个圆柱和一个半球组成,要求半球的半径和圆柱的底面半径之比为3:2,工艺品的体积为34πcm3.设圆柱的底面直径为4x(cm),工艺品的表面积为S(cm2).