题目内容
【题目】已知椭圆
，抛物线
的焦点均在
轴上，的中心和的顶点均为原点
，从每条曲线上各取两个点，其坐标分别是
，
，
，
．
（
）求，的标准方程．
（
）过点
的直线
与椭圆交于不同的两点
，
，且
为锐角（其中为坐标原点），求直线的斜率
的取值范围．
【答案】（1）
，
（2）
或
．
【解析】
(1) 根据题意布列关于待定系数的方程组，解之即可;
(2) 设直线l：y＝kx+2，A（x1，y1），B（x2，y2），由
，得（1+4k2）x2+16kx+12＝0，由此利用根的判别式、韦达定理、向量的数量积，结合已知条件能求出直线l的斜率k的取值范围．
解：（
）由题意抛物线的顶点为原点，
所以点
一定在椭圆上，且
，则椭圆上任何点的横坐标的绝对值都小于等于
，
所以
也在椭圆上，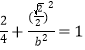
，
，故椭圆标准方程，
所以点
、
在抛物线上，且抛物线开口向右，其方程
，
，
，
所以方程为．
（）①当直线
斜率不存在时，易知
三点共线，不符题意．
②当斜率存在时，设
，
，
，
，
，
，
令
，
，
，
或
，
，
，
，
,
,
,
，
令
，
即
，
或．
综上：或．
练习册系列答案
相关题目
