题目内容
已知抛物线y2=4ax(a>0)的焦点为F,以点A(a+4,0)为圆心,|AF|为半径的圆在x轴的上方与抛物线交于M、N两点.(I)求证:点A在以M、N为焦点,且过点F的椭圆上;
(II)设点P为MN的中点,是否存在这样的a,使得|FP|是|FM|与|FN|的等差中项?如果存在,求出实数a的值;如果不存在,请说明理由.
【答案】分析:(1)由题中易知F的坐标为(a,0),故|FA|=4所以,该圆的方程为(x-a-4)2+y2=16.因此要证明点A在以M、N为焦点的椭圆上只需证明|AM|+|AN|=定值且|MN|<|AM|+|AN|即可根据椭圆的定义得出证明.而要证明以M、N为焦点的椭圆过点F
只需证明|FM|+|FN|=定值且|MN|<|FM|+|FN|,而|FM|,|FN|是抛物线的两个过焦点的弦因而根据抛物线的定义可得:|FM|=x1+a,|FN|=x2+a所以|FM|+|FN|=x1+x2+2a所以需要联立方程.
(2)可假设存在这样的a,使得|FP|是|FM|与|FN|的等差中项则2|FP|=|FM|+|FN|=8即|FP|=4.设P的坐标为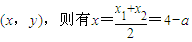 ,
,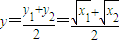 ×
×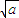 利用两点间的距离公式可得|FP|=4中与x1+x2,x1x2间的关系代入求解即可,要注意在0<a<1的条件下取舍.
利用两点间的距离公式可得|FP|=4中与x1+x2,x1x2间的关系代入求解即可,要注意在0<a<1的条件下取舍.
解答:(本小题满分13分)
解:(I)因为该抛物线的焦点F的坐标为(a,0),故|FA|=4
所以,该圆的方程为(x-a-4)2+y2=16,
它与y2=4ax在x轴的上方交于M(x1,y1),N(x2,y2)(y1>0,y2>0,x1>0,x2>0)
把y2=4ax代入到(x-a-4)2+y2=16中并化简得:
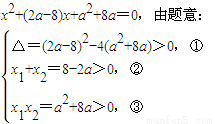
由①②③得0<a<1
又由抛物线定义可得:|FM|=x1+a,|FN|=x2+a
所以|FM|+|FN|=x1+x2+2a=8
而|MN|<|FM|+|FN|=8
又点F,M,N均在圆上,所以,|AN|=|AM|=|AF|=4
所以,|AM|+||AN=8,
因为,|AM|+|AN|=|FM|+|FN|=8,|MN|<8
所以,点A在以M、N为焦点,且过点F的椭圆上,…(8分)
(II)若存在满足条件的实数a,
则有2|FP|=|FM|+|FN|=8⇒|FP|=4
设点P的坐标为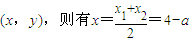
,,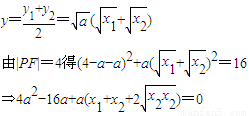
由(2)(3)得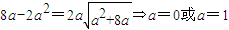
这与0<a<1矛盾
故不存在这样的a,使得|FP|是|FM|与|FN|的等差中项 …(13分)
点评:本题第一问主要考查了利用椭圆的定义来证明点A在以M、N为焦点且过点F的椭圆上关键是|AM|+|AN|=定值且|MN|<|AM|+|AN|和|FM|+|FN|=定值且|MN|<|FM|+|FN|的证明这可以利用椭圆和圆的性质得到.而对于第二问常用假设a存在然后再利用题中的条件求出a但要与a的范围比较,若在此范围内则存在否则不存在.
只需证明|FM|+|FN|=定值且|MN|<|FM|+|FN|,而|FM|,|FN|是抛物线的两个过焦点的弦因而根据抛物线的定义可得:|FM|=x1+a,|FN|=x2+a所以|FM|+|FN|=x1+x2+2a所以需要联立方程.
(2)可假设存在这样的a,使得|FP|是|FM|与|FN|的等差中项则2|FP|=|FM|+|FN|=8即|FP|=4.设P的坐标为
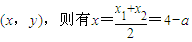 ,
,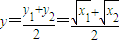 ×
×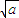 利用两点间的距离公式可得|FP|=4中与x1+x2,x1x2间的关系代入求解即可,要注意在0<a<1的条件下取舍.
利用两点间的距离公式可得|FP|=4中与x1+x2,x1x2间的关系代入求解即可,要注意在0<a<1的条件下取舍.解答:(本小题满分13分)
解:(I)因为该抛物线的焦点F的坐标为(a,0),故|FA|=4
所以,该圆的方程为(x-a-4)2+y2=16,
它与y2=4ax在x轴的上方交于M(x1,y1),N(x2,y2)(y1>0,y2>0,x1>0,x2>0)
把y2=4ax代入到(x-a-4)2+y2=16中并化简得:
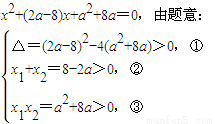
由①②③得0<a<1
又由抛物线定义可得:|FM|=x1+a,|FN|=x2+a
所以|FM|+|FN|=x1+x2+2a=8
而|MN|<|FM|+|FN|=8
又点F,M,N均在圆上,所以,|AN|=|AM|=|AF|=4
所以,|AM|+||AN=8,
因为,|AM|+|AN|=|FM|+|FN|=8,|MN|<8
所以,点A在以M、N为焦点,且过点F的椭圆上,…(8分)
(II)若存在满足条件的实数a,
则有2|FP|=|FM|+|FN|=8⇒|FP|=4
设点P的坐标为
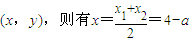
,,
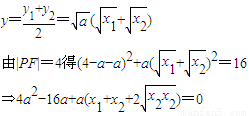
由(2)(3)得
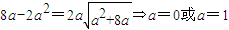
这与0<a<1矛盾
故不存在这样的a,使得|FP|是|FM|与|FN|的等差中项 …(13分)
点评:本题第一问主要考查了利用椭圆的定义来证明点A在以M、N为焦点且过点F的椭圆上关键是|AM|+|AN|=定值且|MN|<|AM|+|AN|和|FM|+|FN|=定值且|MN|<|FM|+|FN|的证明这可以利用椭圆和圆的性质得到.而对于第二问常用假设a存在然后再利用题中的条件求出a但要与a的范围比较,若在此范围内则存在否则不存在.

练习册系列答案
相关题目

 ,过抛物线C1的焦点F作倾斜角为
,过抛物线C1的焦点F作倾斜角为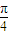 的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线C1于一点Q(点Q在x轴下方).
的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线C1于一点Q(点Q在x轴下方).