��Ŀ����
��֧��һ�и߶����ѧ���ǰ����������ǰ���������е��飬��������40�ˣ���������25�ˣ�Ů��15�ˣ���������15�˰�������������10�˰������飮Ů������5�˰�������������10�˰������飻
��1������������������һ��2��2����������
��2����Ҫ�Ӱ��������ʹӰ��������ѧ���и�ѡһ�˷ֱ���������Э���ˣ���ѡ��������ǡ����һ��һŮ�ĸ��ʣ�
��3���ڶ��ij̶��Ͽ�����Ϊ�Ա����Ƿ������й�ϵ��
����K2=
���˹�ʽҲ��д��X2=
��
�ο����ݣ�
��1������������������һ��2��2����������
��2����Ҫ�Ӱ��������ʹӰ��������ѧ���и�ѡһ�˷ֱ���������Э���ˣ���ѡ��������ǡ����һ��һŮ�ĸ��ʣ�
��3���ڶ��ij̶��Ͽ�����Ϊ�Ա����Ƿ������й�ϵ��
����K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
�ο����ݣ�
| P��K2��k�� | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
�����ݹ�������40�ˣ���������25�ˣ�Ů��15�ˣ���������15�˰�������������10�˰������飮Ů������5�˰�������������10�˰������飬�õ���������
����������֪������һ���ȿ����¼��ĸ��ʣ�
���鷢���������¼���20��20
�����������¼�����15��10+5��10
��ǡ����һ��һŮ�ĸ����ǣ�
=
����K2=
=
=
=2.6666��2.072
��P��K2��2.072��=0.15
����85%�İ��տ�����Ϊ�Ա����Ƿ��ϲ�������й�ϵ��
| �������� �Ա� |
�������� |
�������� |
�ϼ� |
| ���� | 15 | 10 | 25 |
| �� | 5 | 10 | 15 |
| �ϼ� | 20 | 20 | 40 |
���鷢���������¼���20��20
�����������¼�����15��10+5��10
��ǡ����һ��һŮ�ĸ����ǣ�
| 15��10+5��10 |
| 20��20 |
| 1 |
| 2 |
����K2=
| n(ac-bd)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 40��(15��10-5��10)2 |
| (15+10)(5+10)(15+5)(10+10) |
| 8 |
| 3 |
��P��K2��2.072��=0.15
����85%�İ��տ�����Ϊ�Ա����Ƿ��ϲ�������й�ϵ��

��ϰ��ϵ�д�
�����Ŀ
��֧��һ�и߶����ѧ���ǰ����������ǰ���������е��飬��������40�ˣ���������25�ˣ�Ů��15�ˣ���������15�˰�������������10�˰������飮Ů������5�˰�������������10�˰������飻
��1������������������һ��2��2����������
��2����Ҫ�Ӱ��������ʹӰ��������ѧ���и�ѡһ�˷ֱ���������Э���ˣ���ѡ��������ǡ����һ��һŮ�ĸ��ʣ�
��3���ڶ��ij̶��Ͽ�����Ϊ�Ա����Ƿ������й�ϵ��
����K2=
���˹�ʽҲ��д��X2=
��
�ο����ݣ�
��1������������������һ��2��2����������
��2����Ҫ�Ӱ��������ʹӰ��������ѧ���и�ѡһ�˷ֱ���������Э���ˣ���ѡ��������ǡ����һ��һŮ�ĸ��ʣ�
��3���ڶ��ij̶��Ͽ�����Ϊ�Ա����Ƿ������й�ϵ��
����K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
�ο����ݣ�
| P��K2��k�� | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
�ԡ��ĵ���У���ĸ߶����ѧ���ǰ����������ǰ���������е��飬��������40�ˣ���������25�ˣ�Ů��15�ˡ���������15�˰�������������10�˰������顣Ů������5�˰�������������10�˰������飻
��1������������������һ��2��2����������
��2���ڶ��ij̶��Ͽ�����Ϊ�Ա����Ƿ������й�ϵ��
���� ���˹�ʽҲ��д��
���˹�ʽҲ��д�� ��
��
�ο����ݣ�
|
|
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
|
|
1.323 |
2.072 |
2. 706 |
3. 841 |
5. 024 |
��֧��һ�и߶����ѧ���ǰ����������ǰ���������е��飬��������40�ˣ���������25�ˣ�Ů��15�ˣ���������15�˰�������������10�˰������飮Ů������5�˰�������������10�˰������飻
��1������������������һ��2��2����������
��2����Ҫ�Ӱ��������ʹӰ��������ѧ���и�ѡһ�˷ֱ���������Э���ˣ���ѡ��������ǡ����һ��һŮ�ĸ��ʣ�
��3���ڶ��ij̶��Ͽ�����Ϊ�Ա����Ƿ������й�ϵ��
����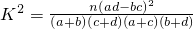 ���˹�ʽҲ��д��
���˹�ʽҲ��д��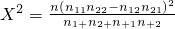 ��
��
�ο����ݣ�
| P��K2��k�� | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
�ԡ��ĵ���У���ĸ߶����ѧ���ǰ����������ǰ���������е��飬��������40�ˣ���������25�ˣ�Ů��15�ˡ���������15�˰�������������10�˰������顣Ů������5�˰�������������10�˰������飻
��1������������������һ��2��2����������
��2���ڶ��ij̶��Ͽ�����Ϊ�Ա����Ƿ������й�ϵ��
���� ���˹�ʽҲ��д��
���˹�ʽҲ��д�� ��
��
�ο����ݣ�
|
|
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
|
|
1.323 |
2.072 |
2. 706 |
3. 841 |
5. 024 |