Question

已知函数y=f（x）的图象可由y=sinx的图象经过如下变换得到：
①将y=sinx的图象的纵坐标保持不变，横坐标缩短为原来的

2

π

；
②将①中的图象整体向左平移

2

3

个单位；
③将②中的图象的横坐标保持不变，纵坐标伸长为原来的

3

倍．
（Ⅰ）求f（x）的周期和单调减区间
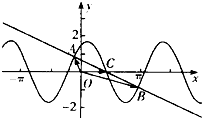
（Ⅱ）函数f（x）的部分图象如图所示，若直线x-2y-

4

3

=0与函数y=f（x）的图象交于A，B，C三点，试求：

OC

•(

OA

+

OB

)的值．

Answer 1

分析：（Ⅰ）由图象变换的知识可得f（x）=

3

sin（

π

2

x+

π

3

），易得周期和单调递减区间；（Ⅱ）设A（x₁，y₁），B（x₂，y₂），由题意可得C（

4

3

，0），易知C恰好为函数f（x）图象的一个对称中心，可得x₁+x₂=

8

3

，y₁+y₂=0，由向量的坐标运算可得答案．

解答：解：（Ⅰ）由图象变换的知识可得：y=sinx的图象经过①的变换可得到y=sin

π

2

x的图象，
再经过②的变换可得到y=sin

π

2

(x+

2

3

)的图象，经过③的变换后得到y=

3

sin

π

2

(x+

2

3

)的图象，
∴y=f（x）=

3

sin

π

2

(x+

2

3

)=

3

sin（

π

2

x+

π

3

），
∴周期T=

2π

π 2

=4，由2kπ+

π

2

≤

π

2

x+

π

3

≤2kπ+

3π

2

可得4k+

1

3

≤x≤4k+

7

3

，
∴函数f（x）的单调递减区间为：[4k+

1

3

，4k+

7

3

]（k∈Z）
（Ⅱ）设A（x₁，y₁），B（x₂，y₂），
由题意知C为直线x-2y-

4

3

=0与x轴的交点，故C（

4

3

，0），
易知C恰好为函数f（x）图象的一个对称中心，
故x₁+x₂=

8

3

，y₁+y₂=0，
∴

OC

•(

OA

+

OB

)=（

4

3

，0）•（

8

3

，0）=

32

9

点评：本题考查平面向量数量积的运算，涉及三角函数图象的变换和单调性，属中档题．