题目内容
.(本题满分14分)
已知直线
 所经过的定点
所经过的定点 恰好是椭圆
恰好是椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆 上的点到点
上的点到点 的最大距离为3.
的最大距离为3.
(Ⅰ) 求椭圆 的标准方程;
的标准方程;
(Ⅱ) 设过点 的直线
的直线 交椭圆于
交椭圆于 、
、 两点,若
两点,若 ,求直线
,求直线 的斜率的取值范围.
的斜率的取值范围.
已知直线

 所经过的定点
所经过的定点 恰好是椭圆
恰好是椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆 上的点到点
上的点到点 的最大距离为3.
的最大距离为3.(Ⅰ) 求椭圆
 的标准方程;
的标准方程;(Ⅱ) 设过点
 的直线
的直线 交椭圆于
交椭圆于 、
、 两点,若
两点,若 ,求直线
,求直线 的斜率的取值范围.
的斜率的取值范围.(Ⅰ)由 得
得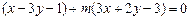 ,
,
由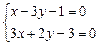 ,解得
,解得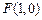 . 2分
. 2分
设椭圆 的标准方程为
的标准方程为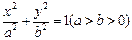 ,则
,则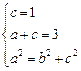 解得
解得 ,
,
从而椭圆 的标准方程为
的标准方程为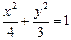 . 6分
. 6分
(Ⅱ) 过 的直线
的直线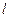 的方程为
的方程为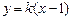 ,
,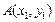 ,
,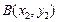 ,
,
由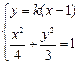 ,得
,得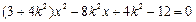 ,因点
,因点 在椭圆内部必有
在椭圆内部必有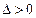 ,
,
有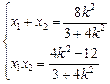 , 8分
, 8分
所以|FA|·|FB| =(1 + k2 )|(x1 – 1)(x2 – 1 )|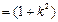
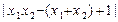
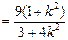 11分
11分
由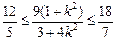 ,得
,得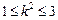 , 解得
, 解得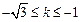 或
或 ,
,
所以直线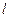 的斜率的取值范围为
的斜率的取值范围为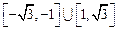 . 14分
. 14分
 得
得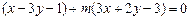 ,
,由
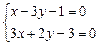 ,解得
,解得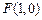 . 2分
. 2分设椭圆
 的标准方程为
的标准方程为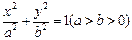 ,则
,则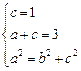 解得
解得 ,
,从而椭圆
 的标准方程为
的标准方程为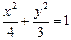 . 6分
. 6分(Ⅱ) 过
 的直线
的直线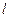 的方程为
的方程为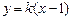 ,
,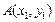 ,
,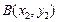 ,
,由
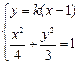 ,得
,得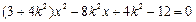 ,因点
,因点 在椭圆内部必有
在椭圆内部必有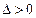 ,
,有
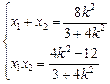 , 8分
, 8分所以|FA|·|FB| =(1 + k2 )|(x1 – 1)(x2 – 1 )|
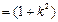
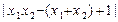
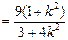 11分
11分由
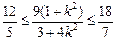 ,得
,得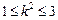 , 解得
, 解得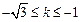 或
或 ,
,所以直线
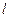 的斜率的取值范围为
的斜率的取值范围为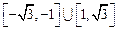 . 14分
. 14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是半圆
是半圆 的直径,点
的直径,点 在半圆上,
在半圆上, 于点
于点 ,且
,且 ,设
,设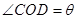 ,则
,则 =( )
=( )




 为
为 △ABC的外接圆,AB=AC,过点A的直线交⊙O于D,交BC延长线
△ABC的外接圆,AB=AC,过点A的直线交⊙O于D,交BC延长线 于F,DE是BD的延长线,连接CD。
于F,DE是BD的延长线,连接CD。
 是圆
是圆 的直径,
的直径,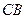 切圆
切圆 点,
点, 切圆
切圆 点,交
点,交 的延长线于E点,
的延长线于E点, 则
则 =____________;
=____________;
 ,设该圆过点
,设该圆过点 的最长弦和最短弦分别为
的最长弦和最短弦分别为 和
和 ,则四边形
,则四边形 的面积为
的面积为  ,则它的内切圆半径为 ( )
,则它的内切圆半径为 ( )

 ,且圆心在直线
,且圆心在直线 上的圆的方程是
上的圆的方程是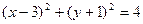



 的直径
的直径 ,
, 为圆周上一点,
为圆周上一点, ,过
,过 ,过
,过 作直线
作直线 ,
, 为垂足,
为垂足, ,则线段
,则线段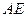 的长为 .
的长为 .