题目内容
已知,数列![]() 有
有![]() (常数
(常数![]() ),对任意的正整数
),对任意的正整数![]()
![]() ,并有
,并有![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)试确定数列![]() 是不是等差数列,若是,求出其通项公式;若不是,说明理由;
是不是等差数列,若是,求出其通项公式;若不是,说明理由;
(3)对于数列![]() ,例如存在一个常数
,例如存在一个常数![]() 使得对任意的正整数
使得对任意的正整数![]() 都有
都有![]() 且
且![]() ,则称
,则称![]() 为数列
为数列![]() 的“上渐进值”,令
的“上渐进值”,令![]() ,求数列
,求数列![]() 的“上渐进值”.
的“上渐进值”.
(1)0(2)是,![]()
(3)3
解析:
(1)由已知,得![]()
(2)由![]() 得
得![]() ,则
,则![]() ,
,
![]()
即![]() ,
,
于是有![]() ,且有
,且有![]()
![]()
即![]() ,
,
则对任意的![]() 都有
都有![]() ,
,
所以,数列![]() 是等差数列,其通项公式是
是等差数列,其通项公式是![]()
(3)![]()
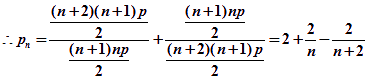
![]()
![]()
由![]() 是正整数可得,
是正整数可得,![]()
并且有![]()
所以数列![]() 的“上渐进值”为3.
的“上渐进值”为3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
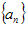 有
有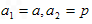 (常数
(常数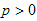 ),对任意的正整数
),对任意的正整数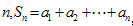 ,并有
,并有 满足
满足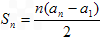 。
。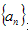 是不是等差数列,若是,求出其通项公式。若不是,说明理由;
是不是等差数列,若是,求出其通项公式。若不是,说明理由;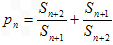 ,是否存在正整数M,使不等式
,是否存在正整数M,使不等式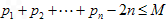 恒成立,若存在,求出M的最小值,若不存在,说明理由。
恒成立,若存在,求出M的最小值,若不存在,说明理由。