题目内容
已知圆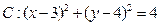 ,直线
,直线 过定点A(1,0).
过定点A(1,0).
(1)若 与圆相切,求
与圆相切,求 的方程;
的方程;
(2)若 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又 与
与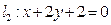 的交点为N,判断
的交点为N,判断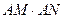 是否为定值,若是,则求出定值;若不是,请说明理由.
是否为定值,若是,则求出定值;若不是,请说明理由.
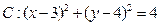 ,直线
,直线 过定点A(1,0).
过定点A(1,0).(1)若
 与圆相切,求
与圆相切,求 的方程;
的方程;(2)若
 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又 与
与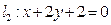 的交点为N,判断
的交点为N,判断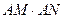 是否为定值,若是,则求出定值;若不是,请说明理由.
是否为定值,若是,则求出定值;若不是,请说明理由.(1)直线方程是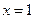 ,
,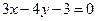 (2)6
(2)6
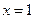 ,
,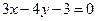 (2)6
(2)6(1)①若直线 的斜率不存在,即直线是
的斜率不存在,即直线是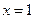 ,符合题意.
,符合题意.
②若直线 斜率存在,设直线
斜率存在,设直线 为
为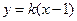 ,即
,即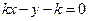 .
.
由题意知,圆心(3,4)到已知直线 的距离等于半径2,即:
的距离等于半径2,即: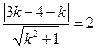 ,
,
解之得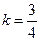 。
。
所求直线方程是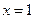 ,
,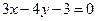 。
。
(2)直线与圆相交,斜率必定存在,且不为0,可设直线方程为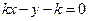
由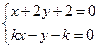 得
得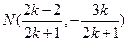 .
.
又直线CM与 垂直,
垂直,
由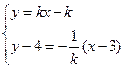 得
得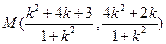 .
.
∴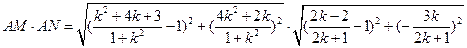
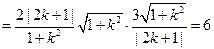 为定值。
为定值。
故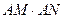 是定值,且为6。
是定值,且为6。
 的斜率不存在,即直线是
的斜率不存在,即直线是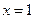 ,符合题意.
,符合题意. ②若直线
 斜率存在,设直线
斜率存在,设直线 为
为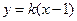 ,即
,即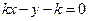 .
.由题意知,圆心(3,4)到已知直线
 的距离等于半径2,即:
的距离等于半径2,即: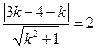 ,
,解之得
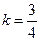 。
。 所求直线方程是
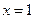 ,
,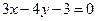 。
。 (2)直线与圆相交,斜率必定存在,且不为0,可设直线方程为
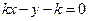
由
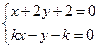 得
得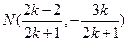 .
. 又直线CM与
 垂直,
垂直,由
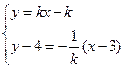 得
得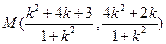 .
. ∴
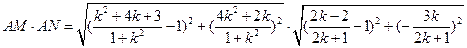
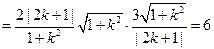 为定值。
为定值。 故
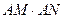 是定值,且为6。
是定值,且为6。 
练习册系列答案
相关题目
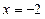 相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线
相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线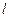 与轨迹C交于A、B两点,且这两点的横坐标分别为
与轨迹C交于A、B两点,且这两点的横坐标分别为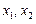 .①求证:
.①求证: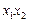 为定值;②试用
为定值;②试用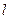 :
: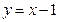 被圆C所截得的弦长为
被圆C所截得的弦长为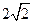 ,则过圆心且与直线
,则过圆心且与直线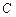 点在⊙
点在⊙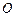 直径的延长线上,
直径的延长线上,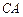 切⊙
切⊙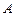 点,
点,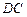 是
是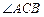 的平分线,且交
的平分线,且交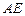 于
于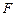 点,交
点,交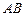 于
于 点.
点.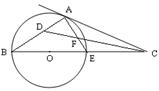
 的度数;
的度数; ,求
,求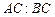 .
.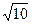 ,圆心在直线
,圆心在直线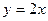 上,圆被直线
上,圆被直线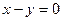 截得的弦长为
截得的弦长为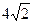 ,求圆的方程.
,求圆的方程.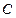 的圆心在直线
的圆心在直线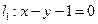 上,圆
上,圆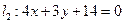 相切,
相切,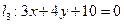 所得弦长为
所得弦长为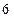 ,求圆
,求圆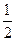
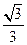
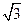
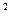 +y
+y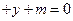 和它关于直线
和它关于直线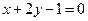 的对称曲线总有交点,那么m的取值范围是__________。
的对称曲线总有交点,那么m的取值范围是__________。