题目内容
已知(x+
)n展开式中,第二项、第三项、第四项的二项式系数成等差数列,则在(x+
)n展开式中系数最大项是( )
| 2 | ||
|
| 2 | ||
|
| A.第3项 | B.第4项 | C.第5项 | D.第6项 |
由题意可得 2
=
+
,解得 n=7.
在(x+
)n=(x+
)7的开式的通项公式为 Tr+1=
•x7-r•2r•x-
=2r•
•x7-
,
故第r+1项的系数为2r•
.
令
,可得整数r=5,
故所求的系数最大项为第六项,
故选D.
| C | 2n |
| C | 1n |
| C | 3n |
在(x+
| 2 | ||
|
| 2 | ||
|
| C | r7 |
| r |
| 2 |
| C | r7 |
| 3r |
| 2 |
故第r+1项的系数为2r•
| C | r7 |
令
|
故所求的系数最大项为第六项,
故选D.

练习册系列答案
相关题目
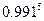 的近似值(精确到
的近似值(精确到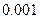 )是多少?
)是多少?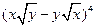 的展开式中
的展开式中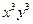 的系数为 .
的系数为 .