题目内容
某考生打算从7所重点大学中选3所填在第一档次的3个志愿栏内,其中A校定为第一志愿,再从5所一般大学中选3所填在第二档次的3个志愿栏内,其中B、C校必选,且B在C前,问此考生共有 种不同的填表方法(用数字作答).
【答案】分析:本题是一个分步计数问题,A校定为第一志愿,从6所大学中选两个在两个位置全排列,B、C校必选,且B在C前,从余下的三个学校选一个,且B在C前面,只要排列后除以2即可,根据分步乘法得到结果.
解答:解:由题意知本题是一个分步计数问题,
∵A校定为第一志愿,
∴从6所大学中选两个在两个位置全排列,共有A62=30种结果,
∵B、C校必选,且B在C前,
∴从余下的三个学校选一个,且B在C前面,只要排列后除以2即可,共有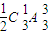 =9种结果,
=9种结果,
根据分步计数原理知共有30×9=270种结果,
故答案为:270.
点评:本题考查分步计数问题,解题时一定要分清做这件事需要分为几步,每一步包含几种方法,再根据分步乘法原理得到结果.本题是一个典型的排列组合的实际应用.
解答:解:由题意知本题是一个分步计数问题,
∵A校定为第一志愿,
∴从6所大学中选两个在两个位置全排列,共有A62=30种结果,
∵B、C校必选,且B在C前,
∴从余下的三个学校选一个,且B在C前面,只要排列后除以2即可,共有
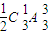 =9种结果,
=9种结果,根据分步计数原理知共有30×9=270种结果,
故答案为:270.
点评:本题考查分步计数问题,解题时一定要分清做这件事需要分为几步,每一步包含几种方法,再根据分步乘法原理得到结果.本题是一个典型的排列组合的实际应用.

练习册系列答案
相关题目