题目内容
下列给出的四个命题中:①已知数列{an},那么对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上是{an}为等差数列的充分不必要条件;
②“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的必要不充分条件;
③设圆x2+y2+Dx+Ey+F=0与坐标轴有4个交点,分别为A(x1,0),B(x2,0),C(0,y1),D(0,y2),则x1x2-y1y2=0;
④在实数数列{an}中,已知a1=0,|a2|=|a1-1|,|a3|=|a2-1|,…,|an|=|an-1-1|,则a1+a2+a3+a4的最大值为2.
其中为真命题的是
分析:①由点Pn(n,an)都在直线y=2x+1上得到an=2n+1,由通项公式知是充分,但反之等差数列很多,是不必要的.
②若“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”则有:(m+2)(m-2)+(m+2)m=0整理得(m+2)(2m-1)=0有两个根.③令x=0,x2+y2+Dx+Ey+F=0化为:y2+Ey+F=0由韦达定理得y1y2=F;令y=0,x2+y2+Dx+Ey+F=0化为:x2+Dx+F=0由韦达定理得x1x2=F,从而有x1x2-y1y2=0;
④由“a1=0,|a2|=|a1-1|,|a3|=|a2-1|,…,|an|=|an-1-1|,”得数列是:0,1,0,1,0,1,…0,1…从而得到结论.
②若“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”则有:(m+2)(m-2)+(m+2)m=0整理得(m+2)(2m-1)=0有两个根.③令x=0,x2+y2+Dx+Ey+F=0化为:y2+Ey+F=0由韦达定理得y1y2=F;令y=0,x2+y2+Dx+Ey+F=0化为:x2+Dx+F=0由韦达定理得x1x2=F,从而有x1x2-y1y2=0;
④由“a1=0,|a2|=|a1-1|,|a3|=|a2-1|,…,|an|=|an-1-1|,”得数列是:0,1,0,1,0,1,…0,1…从而得到结论.
解答:解:∵点Pn(n,an)都在直线y=2x+1上
∴an=2n+1
∴{an}是以3为首项,以2为公差的等差数列
所以是充分的
若{an}为等差数列,则公差不一定为2,首项也不一定为3
所以是不必要的
故①正确.
②若“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”
则有:(m+2)(m-2)+(m+2)m=0
∴(m+2)(2m-1)=0
∴m=-2或m=
故②不正确.
令x=0,x2+y2+Dx+Ey+F=0化为:y2+Ey+F=0
由韦达定理
y1y2=F
令y=0,x2+y2+Dx+Ey+F=0化为:x2+Dx++F=0
由韦达定理
x1x2=F
∴x1x2-y1y2=0;
故③正确
由“a1=0,|a2|=|a1-1|,|a3|=|a2-1|,…,|an|=|an-1-1|,”
可推知数列是:0,1,0,1,0,1,…0,1…
∴a1+a2+a3+a4的最大值为2.
故④正确.
故答案为:①③④
∴an=2n+1
∴{an}是以3为首项,以2为公差的等差数列
所以是充分的
若{an}为等差数列,则公差不一定为2,首项也不一定为3
所以是不必要的
故①正确.
②若“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”
则有:(m+2)(m-2)+(m+2)m=0
∴(m+2)(2m-1)=0
∴m=-2或m=
| 1 |
| 2 |
故②不正确.
令x=0,x2+y2+Dx+Ey+F=0化为:y2+Ey+F=0
由韦达定理
y1y2=F
令y=0,x2+y2+Dx+Ey+F=0化为:x2+Dx++F=0
由韦达定理
x1x2=F
∴x1x2-y1y2=0;
故③正确
由“a1=0,|a2|=|a1-1|,|a3|=|a2-1|,…,|an|=|an-1-1|,”
可推知数列是:0,1,0,1,0,1,…0,1…
∴a1+a2+a3+a4的最大值为2.
故④正确.
故答案为:①③④
点评:本题主要考查数列与函数,方程及逻辑用语的综合运用,主要涉及了等差数列的定义及通项公式,圆的方程及韦达定理和数列规律的探究.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在下列给出的四个命题中,为真命题的是( )
| A、?a∈R,?b∈Q,a2+b2=0 | B、?a∈R,?b∈Q,a2+b2=1 | C、?n∈Z,?m∈Z,n>m2 | D、?n∈N*,?m∈Z,nm=m |
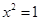 ,则
,则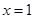 ”的否命题是“若
”的否命题是“若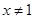 ”;
”;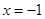 ”是“
”是“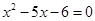 ”的必要不充分条件;
”的必要不充分条件;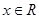 ,使得
,使得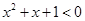 ”的否定是“对任意
”的否定是“对任意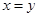 ,则
,则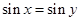 ”的逆否命题为真.
”的逆否命题为真.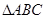 中,
中,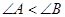 的充要条件是
的充要条件是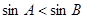 ;
;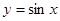 的图像和函数
的图像和函数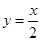 的图像只有一个公共点;
的图像只有一个公共点;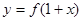 的图像与函数
的图像与函数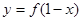 的图像关于直线
的图像关于直线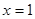 对称;
对称;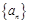 中,已知
中,已知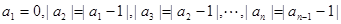
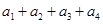 的最大值为2.
的最大值为2.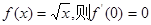
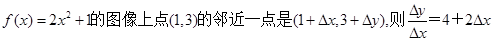
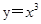 在点(0,0)处没有切线
在点(0,0)处没有切线