题目内容
(1)
满足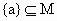
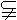 {a,b,c,d}的集合M共有
{a,b,c,d}的集合M共有
[
]|
A .6个 |
B .7个 |
C .8个 |
D .15个 |
(2)
设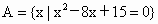 ,
,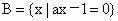 ,若
,若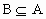 ,求实数a组成的集合,并写出它的所有非空真子集.
,求实数a组成的集合,并写出它的所有非空真子集.
答案:略
解析:
解析:
|
(1) 用子集及真子集的概念来解决.∵ 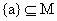 ,∴M中至少含有一个元素a, ,∴M中至少含有一个元素a,
又∵ M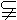 {a,b,c,d},∴M中至多含有三个元素. {a,b,c,d},∴M中至多含有三个元素.
由此可知满足条件的集合 M有{a},{a,b},{a,c},{a,d},{a,b,c},{a,b,d},{a,c,d}共7个.∴选B.(2) 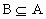 , ,
①若 B=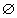 ,则a=0; ,则a=0;
②若 B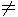 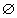 ,则a ,则a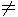 0,这时有 0,这时有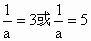 ,即 ,即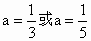 . .
综上所述,由实数 a组成的集合为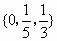 . .
其所有的非空真子集为{0},  , ,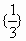 , ,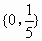 , ,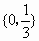 , ,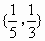 共6个. 共6个. |

练习册系列答案
相关题目
若向量
、
满足|
|=|
|=1,
与
的夹角为60°,则
•
+
•
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| a |
| b |
A、
| ||||
B、
| ||||
C、1+
| ||||
| D、2 |
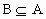

 {a,b,c,d}的集合M共有
{a,b,c,d}的集合M共有 ,
, ,若
,若 ,求实数a组成的集合,并写出它的所有非空真子集.
,求实数a组成的集合,并写出它的所有非空真子集.