题目内容
已知曲线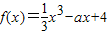 在x=1处的切线方程是y=-3x+b.
在x=1处的切线方程是y=-3x+b.(1)求实数a和b的值;
(2)若函数y=f(x)-m在区间(0,+∞)上有零点,求实数m的取值范围.
【答案】分析:(1)利用曲线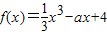 在x=1处的切线方程是y=-3x+b,结合导数的几何意义,列出方程,解出a、b即可;
在x=1处的切线方程是y=-3x+b,结合导数的几何意义,列出方程,解出a、b即可;
(2)函数y=f(x)-m在区间(0,+∞)上有零点,即方程函数f(x)=m在区间(0,+∞)上有解,故只须m在函数y=f(x)(x∈(0,+∞))的值域内即可,故利用导数求函数y=f(x)(x∈(0,+∞))的最值即可.
解答: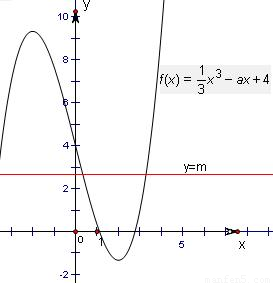 解:(1)∵
解:(1)∵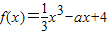 ,∴f'(x)=x2-a,依题意得
,∴f'(x)=x2-a,依题意得
∴f′(1)=1-a=-3,∴a=4;
又可得切点坐标为(1, ),代入切线的方程y=-3x+b,得b=
),代入切线的方程y=-3x+b,得b=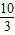 .
.
(2)由f'(x)=x2-4=(x+2)(x-2),令f'(x)=0
解得x=-2或x=2;当f'(x)>0时,解得 x<-2或x>2;当f'(x)<0,解得-2<x<2.
∴f(x)在(0,2)递减,在(2,+∞)上递增,
故f(2)=- 为最小值.
为最小值.
要使y=f(x)-m在区间(0,+∞)上有零点,
则m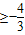 .
.
点评:本题考查利用导数研究曲线上某点切线方程,导数的综合运用以及数形结合的运用能力,对学生有一定的能力要求,有一定的难度.
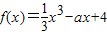 在x=1处的切线方程是y=-3x+b,结合导数的几何意义,列出方程,解出a、b即可;
在x=1处的切线方程是y=-3x+b,结合导数的几何意义,列出方程,解出a、b即可;(2)函数y=f(x)-m在区间(0,+∞)上有零点,即方程函数f(x)=m在区间(0,+∞)上有解,故只须m在函数y=f(x)(x∈(0,+∞))的值域内即可,故利用导数求函数y=f(x)(x∈(0,+∞))的最值即可.
解答:
 解:(1)∵
解:(1)∵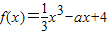 ,∴f'(x)=x2-a,依题意得
,∴f'(x)=x2-a,依题意得∴f′(1)=1-a=-3,∴a=4;
又可得切点坐标为(1,
 ),代入切线的方程y=-3x+b,得b=
),代入切线的方程y=-3x+b,得b=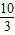 .
.(2)由f'(x)=x2-4=(x+2)(x-2),令f'(x)=0
解得x=-2或x=2;当f'(x)>0时,解得 x<-2或x>2;当f'(x)<0,解得-2<x<2.
∴f(x)在(0,2)递减,在(2,+∞)上递增,
故f(2)=-
 为最小值.
为最小值.要使y=f(x)-m在区间(0,+∞)上有零点,
则m
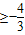 .
.点评:本题考查利用导数研究曲线上某点切线方程,导数的综合运用以及数形结合的运用能力,对学生有一定的能力要求,有一定的难度.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 在x=1处取得极值2,
在x=1处取得极值2, 在x=1处取得极值2,
在x=1处取得极值2,