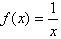题目内容
下列4个命题中,真命题是( )A.如果a>0且a≠1,那么logaf(x)=logag(x)的充要条件是af(x)=ag(x)
B.如果A、B为△ABC的两个内角,那么A>B的充要条件是sinA>sinB
C.如果向量
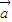 与向量
与向量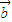 均为非零向量,那么
均为非零向量,那么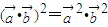
D.函数
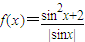 的最小值为
的最小值为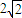
【答案】分析:对于A,直接根据真数大于0即可判断出其不成立;
对于B,结合正弦定理的变形形式即可说明其成立;
对于C,直接根据两个向量数量积的计算公式即可说明其不成立;
对于D,根据基本不等式使用的三个条件中的'相等'这一限制得到其不成立.
解答:解:对于A,logaf(x)=logag(x)?f(x)=g(x)>0,af(x)=ag(x)?f(x)=g(x),∴不成立;
对于B,A、B为△ABC的两个内角,A>B?a>b?2RsinA>2RsinB?sinA>sinB;成立;
对于C,∵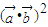 =
=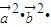 cosθ,∴不成立
cosθ,∴不成立
对于D,∵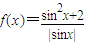 =|sinx|+
=|sinx|+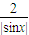 ≥2
≥2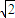 ,取等号时|sinx|=
,取等号时|sinx|=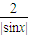 即|sinx|=
即|sinx|=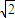 不成立.
不成立.
故选B.
点评:本题是对知识的综合考查.解决此类问题需要有较扎实的基本功,一般这类问题融合的知识点都较多,一个判断出错,整题也就错了,所以也是易错题.
对于B,结合正弦定理的变形形式即可说明其成立;
对于C,直接根据两个向量数量积的计算公式即可说明其不成立;
对于D,根据基本不等式使用的三个条件中的'相等'这一限制得到其不成立.
解答:解:对于A,logaf(x)=logag(x)?f(x)=g(x)>0,af(x)=ag(x)?f(x)=g(x),∴不成立;
对于B,A、B为△ABC的两个内角,A>B?a>b?2RsinA>2RsinB?sinA>sinB;成立;
对于C,∵
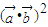 =
=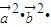 cosθ,∴不成立
cosθ,∴不成立对于D,∵
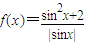 =|sinx|+
=|sinx|+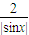 ≥2
≥2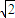 ,取等号时|sinx|=
,取等号时|sinx|=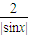 即|sinx|=
即|sinx|=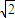 不成立.
不成立.故选B.
点评:本题是对知识的综合考查.解决此类问题需要有较扎实的基本功,一般这类问题融合的知识点都较多,一个判断出错,整题也就错了,所以也是易错题.

练习册系列答案
相关题目