题目内容
【题目】已知![]() ,
, ![]() 是
是![]() 的导函数.
的导函数.
(1)求![]() 的极值;
的极值;
(2)证明:对任意实数![]() ,都有
,都有![]() 恒成立;
恒成立;
(3)若![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)![]() .
.
【解析】试题分析:(Ⅰ)由题意得处![]() ,进而
,进而![]() ,分
,分![]() 和
和![]() 两种情况讨论,即可求解;
两种情况讨论,即可求解;
(Ⅱ)由![]() ,则要证
,则要证![]()
![]() ,只需证
,只需证![]() .
.
令![]() ,利用导数得出函数
,利用导数得出函数![]() 的性质,即可作出证明.
的性质,即可作出证明.
(Ⅲ)由(Ⅱ)知![]() 恒成立,可得
恒成立,可得![]() ,分
,分![]() 和
和![]() 两种情况讨论,即可求解实数
两种情况讨论,即可求解实数![]() 的值.
的值.
试题解析:
(Ⅰ)![]() ,
, ![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 无极值;
无极值;
当![]() 时,
时, ![]() ,即
,即![]() ,
,
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
所以当![]() 时,有极小值
时,有极小值![]() .
.
(Ⅱ)因为![]() ,所以,要证
,所以,要证![]()
![]() ,只需证
,只需证![]() .
.
令![]() ,则
,则![]() ,且
,且![]() ,得
,得![]() ;
; ![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() 恒成立,
恒成立,
∴对任意实数![]() ,都有
,都有![]()
![]() 恒成立.
恒成立.
(Ⅲ)令![]() ,则
,则![]() ,注意到
,注意到![]() ,
,
由(Ⅱ)知![]() 恒成立,故
恒成立,故![]() ,
,
①当![]() 时,
时, ![]() ,
, ![]() ,
,
于是当![]() 时,
时, ![]() ,即
,即![]() 成立.
成立.
②当![]() 时,由
时,由![]() (
(![]() )可得
)可得![]() (
(![]() ).
).
![]() ,
,
故当![]() 时,
时, ![]() ,
,
于是当![]() 时,
时, ![]() ,
, ![]() 不成立.
不成立.
综上, ![]() 的取值范围为
的取值范围为![]() .
.

【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
![]() 的浓度;
的浓度;
(ii)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
参考公式:回归直线的方程是![]() ,其中
,其中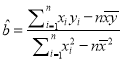 ,
, ![]() .
.
【题目】某研究机构追踪40名小学毕业生随年限与数学水平学习的情况.统计了年限与等级考试的平均成绩,如下列数据:
学习年限 | 2 | 3 | 4 | 5 | 6 |
等级成绩 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)已知![]() 与
与![]() 满足线性关系,试求年限
满足线性关系,试求年限![]() 与等级考试成绩
与等级考试成绩![]() 的线性回归直线方程
的线性回归直线方程![]() .(其中
.(其中 ,
,![]() )
)
(2)如果对40名学生“是否对数学学习感兴趣”进行调查,初中生和高中生对数学的喜欢程度如下联表(其中学习年限2年或3年的为初中阶段,年限为4年或5年或6年的为高中阶段)
喜欢 | 不喜欢 | 合计 | |
初中生 | 8 | 12 | 20 |
高中生 | 16 | 4 | 20 |
合计 | 24 | 16 | 40 |
根据上表计算![]() ,并说明是否有
,并说明是否有![]() 的把握认为“喜欢数学与学习年限有关”(其中
的把握认为“喜欢数学与学习年限有关”(其中![]() 其中
其中![]() )
)
| 0.025 | 0.010 | 0.005 |
| 5.024 | 6.635 | 7.897 |
【题目】“公益行”是由某公益慈善基金发起并主办的一款将用户的运动数据转化为公益步数的捐助公益项目的产品,捐助规则是满10000步方可捐助且个人捐出10000步等价于捐出1元,现粗略统计该项目中其中200名的捐助情况表如下:
捐款金额(单位:元) |
|
|
|
|
|
|
捐款人数 | 4 | 152 | 26 | 10 | 3 | 5 |
(1)将捐款额在200元以上的人称为“健康大使”,请在现有的“健康大使”中随机抽取2人,求捐款额在![]() 之间人数
之间人数![]() 的分布列;
的分布列;
(2)为鼓励更多的人来参加这项活动,该公司决定对捐款额在100元以上的用户实行红包奖励,具体奖励规则如下:捐款额在![]() 的奖励红包5元;捐款额在
的奖励红包5元;捐款额在![]() 的奖励红包8元;捐款额在
的奖励红包8元;捐款额在![]() 的奖励红包10元;捐款额大于250的奖励红包15元.已知该活动参与人数有40万人,将频率视为概率,试估计该公司要准备的红包总金额.
的奖励红包10元;捐款额大于250的奖励红包15元.已知该活动参与人数有40万人,将频率视为概率,试估计该公司要准备的红包总金额.