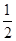题目内容
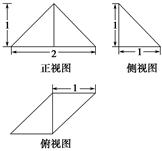
如图所示，在四棱锥P－ABCD中，△PBC为正三角形，PA⊥底面ABCD，其三视图如图所示，俯视图是直角梯形．
(1)求正视图的面积；
(2)求四棱锥P－ABCD的体积．
(1)求正视图的面积；
(2)求四棱锥P－ABCD的体积．
（1）
（2）
（2）(1)如图所示，过A作AE∥CD交BC于E，联结PE.根据三视图可知，E是BC的中点，
且BE＝CE＝1，AE＝CD＝1，
又∵△PBC为正三角形，
∴BC＝PB＝PC＝2，且PE⊥BC.
∴PE2＝PC2－CE2＝3.
∵PA⊥平面ABCD，AE?平面ABCD，∴PA⊥AE，
∴PA2＝PE2－AE2＝2，即PA＝，
∴正视图的面积为S＝
×2×＝.
(2)由(1)可知，四棱锥P－ABCD的高PA＝，
底面积为S＝
·CD＝
×1＝
∴四棱锥P－ABCD的体积V四棱锥P－ABCD＝
S·PA＝××＝.
且BE＝CE＝1，AE＝CD＝1，
又∵△PBC为正三角形，
∴BC＝PB＝PC＝2，且PE⊥BC.
∴PE2＝PC2－CE2＝3.
∵PA⊥平面ABCD，AE?平面ABCD，∴PA⊥AE，
∴PA2＝PE2－AE2＝2，即PA＝
，∴正视图的面积为S＝
×2×＝.(2)由(1)可知，四棱锥P－ABCD的高PA＝
，底面积为S＝
·CD＝×1＝∴四棱锥P－ABCD的体积V四棱锥P－ABCD＝
S·PA＝××＝.
练习册系列答案
阅读快车系列答案
相关题目
和三棱锥
组合而成，点
、
、
在圆
的圆周上，其正（主）视图、侧（左）视图的面积分别为10和12，如图4所示，其中
，
，
，
．
；
的体积．
A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号). 
时,S为四边形;
时,S与C1D1的交点R满足C1R=
;
.
)cm2
