题目内容
已知向量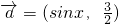 ,
,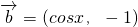
(1)当 ∥
∥ 时,求2cos2x-sin2x的值;
时,求2cos2x-sin2x的值;
(2)求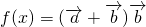 在
在 上的值域.
上的值域.
解:(1)∵ ∥
∥ ,
,
∴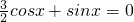 ,
,
∴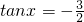 ,(3分)
,(3分)
∴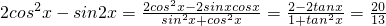 .(6分)
.(6分)
(2)∵ ,
,
∴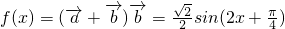 ,(8分)
,(8分)
∵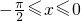 ,∴
,∴ ,
,
∴ ,(10分)
,(10分)
∴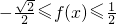 ,(12分)
,(12分)
∴函数f(x)的值域为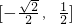 .(13分)
.(13分)
分析:(1)利用向量平行的坐标运算,同角三角函数间的关系,得到tanx的值,然后化简2cos2x-sin2x即可
(2)先表示出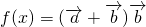 在=
在= (sin2x+
(sin2x+ ),再根据x的范围求出函数f(x)的最大值及最小值.
),再根据x的范围求出函数f(x)的最大值及最小值.
点评:本题主要考查平面向量的坐标运算.考查平面向量时经常和三角函数放到一起做小综合题.是高考的热点问题.
 ∥
∥ ,
,∴
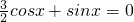 ,
,∴
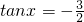 ,(3分)
,(3分)∴
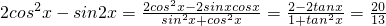 .(6分)
.(6分)(2)∵
 ,
,∴
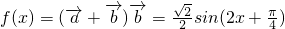 ,(8分)
,(8分)∵
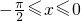 ,∴
,∴ ,
,∴
 ,(10分)
,(10分)∴
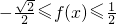 ,(12分)
,(12分)∴函数f(x)的值域为
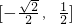 .(13分)
.(13分)分析:(1)利用向量平行的坐标运算,同角三角函数间的关系,得到tanx的值,然后化简2cos2x-sin2x即可
(2)先表示出
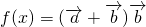 在=
在= (sin2x+
(sin2x+ ),再根据x的范围求出函数f(x)的最大值及最小值.
),再根据x的范围求出函数f(x)的最大值及最小值.点评:本题主要考查平面向量的坐标运算.考查平面向量时经常和三角函数放到一起做小综合题.是高考的热点问题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 ,
, .
. ∥
∥ 时,求
时,求 的值;
的值; 在
在 上的值域.
上的值域. ,
,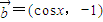
 与向量
与向量 共线时,求tanx的值;
共线时,求tanx的值; )
) 的最大值,并求函数取得最大值时的x的值.
的最大值,并求函数取得最大值时的x的值. ,
,
 与向量
与向量 共线时,求tanx的值;
共线时,求tanx的值; )
) 的最大值,并求函数取得最大值时的x的值.
的最大值,并求函数取得最大值时的x的值. ,
, .
. ∥
∥ 时,求
时,求 的值;
的值; 在
在 上的值域.
上的值域.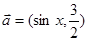 ,
,
 ∥
∥ 时,求
时,求 的值;
的值;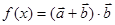 在
在 上的值域.
上的值域.